题目内容
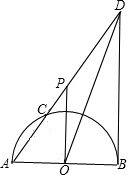 如图,已知:AB为⊙O的直径,AB=6
如图,已知:AB为⊙O的直径,AB=6| 3 |
| 1 |
| 3 |
(1)求OD的长;
(2)若P是AD上的任意一点(不与A、D重合),设PD=x,求△POD的面积y与x的函数关系式,并指出x的取值范围.
分析:(1)连接OC,由弧AC=
弧AB,根据等弧对等角得到∠AOC为60°,又OC=OA,则三角形AOC为等边三角形,得到∠A为60°,在直角三角形ABD中,由锐角三角函数的定义得到tanA等于DB比AB,由tanA和AB的值,求出DB的值,由根据半径OB为直径AB的一半求出OB的长,在直角三角形OBD中,利用勾股定理求出OD的长即可;
(2)过O作OE垂直于AC,即为三角形OPD中PD边上的高,根据等边三角形的性质得到E为AC中点,由AC的长求出AE的长,在直角三角形AEO中,由OA和AE的长,利用勾股定理求出OE的长,利用PD乘以OE的一半即可表示出三角形OPD的面积,得到y与x的关系式,由三角形ABD为直角三角形,且∠ADB为30°,由AB的长,根据直角三角形中,30°角所对的直角边等于斜边的一半求出AD的长,即得到x的范围.
| 1 |
| 3 |
(2)过O作OE垂直于AC,即为三角形OPD中PD边上的高,根据等边三角形的性质得到E为AC中点,由AC的长求出AE的长,在直角三角形AEO中,由OA和AE的长,利用勾股定理求出OE的长,利用PD乘以OE的一半即可表示出三角形OPD的面积,得到y与x的关系式,由三角形ABD为直角三角形,且∠ADB为30°,由AB的长,根据直角三角形中,30°角所对的直角边等于斜边的一半求出AD的长,即得到x的范围.
解答: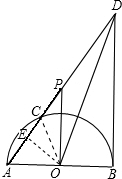 解:(1)连接OC.
解:(1)连接OC.
∵弧AC=
弧AB,
∴∠AOC=
∠AOB=60°,
又OA=OC,
∴△ACO为等边三角形,
∴∠A=60°,
又BD为半圆的切线,
∴BD⊥AB,即∠ABD=90°,
又AB=6
,
在Rt△ABD中,tanA=
,
∴BD=ABtan60°=6
×
=18,
∴∠ADB=30°,
∴AD=2AB=12
,
又半径OB=
AB=3
,
在Rt△OBD中,根据勾股定理得:
OD=
=
=3
;
(2)过O作OE⊥AC,交AC于点E.
∵△ACO为等边三角形,
∴AE=CE=
AC=
,又AO=3
,
在Rt△AEO中,根据勾股定理得:OE=
=
,
则三角形OPD的面积y=
PD•OE=
x•
=
x,且0<x<12
.
 解:(1)连接OC.
解:(1)连接OC.∵弧AC=
| 1 |
| 3 |
∴∠AOC=
| 1 |
| 3 |
又OA=OC,
∴△ACO为等边三角形,
∴∠A=60°,
又BD为半圆的切线,
∴BD⊥AB,即∠ABD=90°,
又AB=6
| 3 |
在Rt△ABD中,tanA=
| DB |
| AB |
∴BD=ABtan60°=6
| 3 |
| 3 |
∴∠ADB=30°,
∴AD=2AB=12
| 3 |
又半径OB=
| 1 |
| 2 |
| 3 |
在Rt△OBD中,根据勾股定理得:
OD=
| BD2+OB2 |
182+(3
|
| 39 |
(2)过O作OE⊥AC,交AC于点E.
∵△ACO为等边三角形,
∴AE=CE=
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
在Rt△AEO中,根据勾股定理得:OE=
(3
|
| 9 |
| 2 |
则三角形OPD的面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
| 3 |
点评:此题考查了等边三角形的判定与性质,切线的性质,勾股定理,圆周角定理,以及锐角三角函数定义,此类题的综合性比较强,要求学生掌握知识全面,借助图形,多次利用转化的思想来求解,培养了学生分析问题,解决问题的能力.

练习册系列答案
相关题目
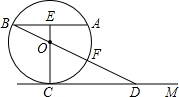 如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
如图,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D. 如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°.
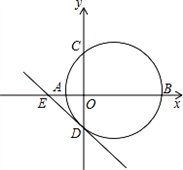
如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°. 如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(-
如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(- ,0).
,0).