题目内容
13.长、宽、高分别为15cm,10cm,20cm的长方体盒子,能放进去的最长的木棍的长度是5$\sqrt{29}$cm.分析 首先利用勾股定理计算出BC的长,再利用勾股定理计算出AB的长即可.
解答  解:∵侧面对角线BC2=152+102,
解:∵侧面对角线BC2=152+102,
∴CB=$\sqrt{325}$cm,
∵AC=20cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{725}$=5$\sqrt{29}$cm,
∴长方体盒子,能放进去的最长的木棍的长度为5$\sqrt{29}$cm,
故答案为:5$\sqrt{29}$cm.
点评 本题重点考查学生的空间想象能力及勾股定理的应用,解题的关键是熟悉勾股定理并两次应用勾股定理,难度一般.

练习册系列答案
相关题目
8.若1<x<2,则$\sqrt{{(x-3)}^{2}}$+$\sqrt{{(x-1)}^{2}}$的值为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
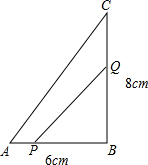 如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B沿边BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.问:
如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B沿边BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.问: