题目内容
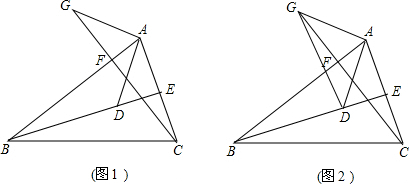
△ABC中，BE，CF是△ABC的角平分线，且BE，CF交于点D，∠A=44°，则∠BDC为
- A.110°
- B.112°
- C.120°
- D.144°
B
分析：本题考查的是三角形内角和定理．主要明确BE，CF是△ABC的角平分线的关系即可求解．
解答：∵∠A=44°，BE，CF是△ABC的角平分线，
∴∠CBE+∠BCF=
（180°-∠A）=68°．
又∵∠CBE+∠BCF+∠BDC=180°，
∴∠BDC=112°．
故选B．
点评：本题运用的是三角形内角和定理．只需画图理解即可．
分析：本题考查的是三角形内角和定理．主要明确BE，CF是△ABC的角平分线的关系即可求解．
解答：∵∠A=44°，BE，CF是△ABC的角平分线，
∴∠CBE+∠BCF=
（180°-∠A）=68°．又∵∠CBE+∠BCF+∠BDC=180°，
∴∠BDC=112°．
故选B．
点评：本题运用的是三角形内角和定理．只需画图理解即可．
练习册系列答案
相关题目
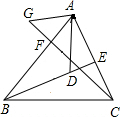已知：如图，在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连AD、AG．求证：AG=AD．
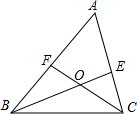知识链接：三角形三个内角的和是180度．（如图∠A是△ABC的一个内角）如图：△ABC中，BE、CF分别是∠ABC和∠ACB的平分线，BE、CF相交于点O．
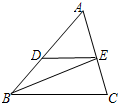（2013•徐汇区一模）如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．