题目内容
16.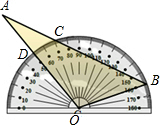 将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A=24°.
将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A=24°.
分析 以EF为直径作半圆,延长BO交圆于M,连接OC,根据已知度数求出∠BOA、∠BOF、∠AOB的度数,根据圆周角定理求出∠B,根据三角形内角和定理求出即可.
解答 解:如图,以EF为直径作半圆,延长BO交圆于M,连接OC,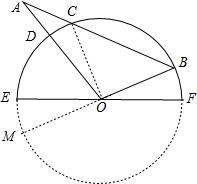
∵点B,C,D对应的读数分别为160°、72°、50°,
∴∠BOA=160°-50°=110°,∠BOF=180°-160°=20°,∠COE=72°,
∴∠COM=72°+20°=92°,
∴∠B=$\frac{1}{2}$∠COM=46°,
∴∠A=180°-∠B-∠AOB=180°-110°-46°=24°.
故答案为:24°.
点评 本题考查了圆周角定理,三角形内角和定理的应用,能求出∠B的度数是解此题的关键.

练习册系列答案
相关题目
 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
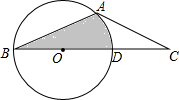 如图,在△ABC中,AB=AC,∠ABC=30°,点O在边BC上,⊙O经过点A,B,且与BC相交于点D.
如图,在△ABC中,AB=AC,∠ABC=30°,点O在边BC上,⊙O经过点A,B,且与BC相交于点D.