题目内容
6.已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点,求该图象与x轴交点的坐标(-2,0).分析 分别把M(0,2),(1,3)代入y=kx+b,根据待定系数法求得一次函数的解析式,然后令y=0,解得即可.
解答 解:把M(0,2),(1,3)代入y=kx+b,
得$\left\{\begin{array}{l}{b=2}\\{k+b=3}\end{array}\right.$,
∴k=1,b=2,
∴一次函数的解析式为y=x+2;
令y=0,则0=x+2,
∴x=-2,
∴交点坐标为(-2,0),
故答案为(-2,0).
点评 本题考查了待定系数法求一次函数解析式:先设一次函数的解析式为y=kx+b,然后把一次函数图象上两点的坐标代入得到关于k、b的方程组,解方程组求出k、b的值,从而确定一次函数的解析式.也考查了一次函数图象上点的坐标特征.

练习册系列答案
相关题目
14.已知|a|=5,|b|=2,则|a-b|的值是( )
| A. | 3 | B. | 7 | C. | 3或7 | D. | ±3或±7 |
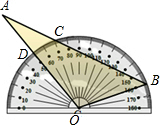 将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A=24°.
将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A=24°.