题目内容
13.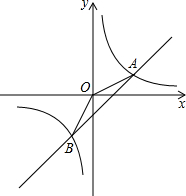 如图:已知反比例函数y1=$\frac{k}{x}$(k为常数,k≠0)的图象与一次函数y2=mx+n (m≠0)交于点A(2,3)、点B(-1,a).
如图:已知反比例函数y1=$\frac{k}{x}$(k为常数,k≠0)的图象与一次函数y2=mx+n (m≠0)交于点A(2,3)、点B(-1,a).(1)求反比例函数和一次函数的关系式;
(2)利用图象直接写出当x在什么范围时,y1>y2.
分析 (1)把点A坐标代入反比例函数求出k的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出a的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)找出直线在反比例函数图形的上方的自变量x的取值即可.
解答 解:(1)∵点A(2,3)在反比例函数y1=$\frac{k}{x}$的图象上,
∴k=2×3=6,
∴反比例函数的表达式为y1=$\frac{6}{x}$,
∵点B(-1,a)也在反比例函数y1=$\frac{6}{x}$的图象上,
∴a=$\frac{6}{-1}$=-6,
即B(-1,-6),
把点A(2,3),点B(-1,-6)代入一次函数y2=mx+n中,
得$\left\{\begin{array}{l}{2m+n=3}\\{-m+n=-6}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=3}\\{n=-3}\end{array}\right.$,
∴一次函数的表达式为y2=3x-3;
(2)根据图象得知:当x<-1或0<x<2时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,此类题目的求解一般都是先把已知点的坐标代入反比例函数表达式求出反比例函数解析式,然后再求一次函数解析式,难度中等.

练习册系列答案
相关题目
18.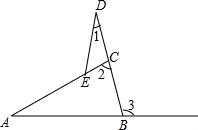 如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
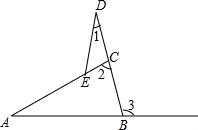 如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )| A. | ∠3>∠2>∠1 | B. | ∠2>∠3>∠1 | C. | ∠3=∠1+∠2 | D. | ∠1+∠2+∠3=180° |
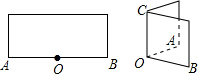 将一张长方形对折,使OA与OB重合,这时∠AOC是什么角?为什么?
将一张长方形对折,使OA与OB重合,这时∠AOC是什么角?为什么? 如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.
如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.