题目内容
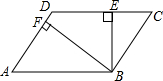 如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=2,DF=1,∠EBF=60°,则这个?ABCD的面积是( )
如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=2,DF=1,∠EBF=60°,则这个?ABCD的面积是( )A、2
| ||
B、2
| ||
C、3
| ||
D、12
|
考点:平行四边形的性质
专题:
分析:求出∠D=120°,根据平行四边形的性质求出∠A=∠C=60°,解直角三角形求出BC=AD=4,求出AF,解直角三角形求出BF,求出面积即可.
解答:解:∵BE⊥CD,BF⊥AD,
∴∠BEC=90°,∠BED=∠BFD=90°,
∵∠EBF=60°,
∴∠D=120°,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠C=180°-∠D=60°,
∴∠A=∠C=60°,
∵CE=2,
∴BC=4,
∴AD=BC=4,
∵DF=1,
∴AF=3,
∴AB=2AE=6,BF=3
,
∴这个?ABCD的面积是AD×BF=4×3
=12
,
故选D.
∴∠BEC=90°,∠BED=∠BFD=90°,
∵∠EBF=60°,
∴∠D=120°,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠C=180°-∠D=60°,
∴∠A=∠C=60°,
∵CE=2,
∴BC=4,
∴AD=BC=4,
∵DF=1,
∴AF=3,
∴AB=2AE=6,BF=3
| 3 |
∴这个?ABCD的面积是AD×BF=4×3
| 3 |
| 3 |
故选D.
点评:本题考查了平行四边形的性质,解直角三角形的应用,注意:平行四边形的对边平行且相等,平行四边形的面积等于底乘以高.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
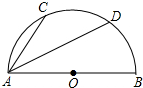 如图所示,半圆O的直径AB=10cm,弦AC=6cm,弦AD平分∠BAC,AD的长为
如图所示,半圆O的直径AB=10cm,弦AC=6cm,弦AD平分∠BAC,AD的长为