题目内容
已知α，β均为锐角，且tanα=
，tanβ=
，求α+β的度数．
【答案】分析：根据两角和的正切公式判断出tan（α+β）的值，进而判断出α+β的度数即可．
解答：解：tan（α+β）=
=
=
=1，
又∵α，β都是锐角，
∴α+β=135°或45°．
∵tanα=
，tanβ=
∴α，β都小于45°
∴α+β=45°．
点评：考查锐角三角函数的知识；掌握两角和的正切公式是解决本题的关键．
解答：解：tan（α+β）=
===1，又∵α，β都是锐角，
∴α+β=135°或45°．
∵tanα=
，tanβ=∴α，β都小于45°
∴α+β=45°．
点评：考查锐角三角函数的知识；掌握两角和的正切公式是解决本题的关键．
练习册系列答案
相关题目
已知p、q均为质数，且满足5p2+3q=59，由以p+3、1-p+q、2p+q-4为边长的三角形是（ ）
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、等腰三角形 |
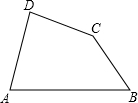已知：如图，在四边形ABCD中，AD=BC，∠A、∠B均为锐角．
均为锐角三角形，
，
，
．
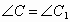作BD⊥CA于D，
于
．
，
，
．