Question

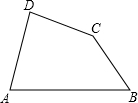已知：如图，在四边形ABCD中，AD=BC，∠A、∠B均为锐角．
（1）当∠A=∠B时，则CD与AB的位置关系是CD

∥

AB，大小关系是CD

＜

AB；
（2）当∠A＞∠B时，（1）中CD与AB的大小关系是否还成立，证明你的结论．

Answer 1

分析：（1）利用∠A、∠B均为锐角，则可延长AD与BC，设它们相交于E点，根据等腰三角形的判定由∠A=∠B得到EA=EB，而AD=BC，则ED=EC，再根据等腰三角形的性质得∠1=∠2，然后利用三角形内角和易得∠1=∠A，根据平行线的判定方法得到CD∥AB；
（2）分别过点D、B作BC、CD的平行线，两线交于F点，根据平行四边形的判定四边形DCBF为平行四边形，再利用平行四边形的性质得FD=BC，DC=FB，由AD=BC得到AD=FD；作∠ADF的平分线交AB于G点，连接GF，则∠ADG=∠FDG，然后根据“SAS”可判断△ADG≌△FDG，则AG=FG，在△BFG中，根据三角形三边的关系得到FG+BG＞BF，于是AG+BG＞DC，即DC＜AB．

解答：解：（1）由于∠A、∠B均为锐角，则延长AD与BC有交点，设它们相交于E点，所以CD＜AB，如图1，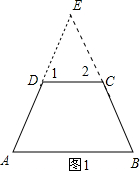
∵∠A=∠B，
∴EA=EB，
∵AD=BC，
∴ED=EC，
∴∠1=∠2，
而∠E+∠A+∠B=∠E+∠1+∠2=180°，
∴∠1=∠A，
∴CD∥AB；

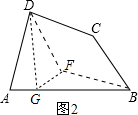（2）答：CD＜AB还成立．
如图2，分别过点D、B作BC、CD的平行线，两线交于F点，作∠ADF的平分线交AB于G点，连接GF，则∠ADG=∠FDG．
∴四边形DCBF为平行四边形．
∴FD=BC，DC=FB，
∵AD=BC
∴AD=FD，
∵在△ADG和△FDG中

AD=FD ∠ADG=∠FDG DG=DG

，
∴△ADG≌△FDG（SAS），
∴AG=FG，
在△BFG中，FG+BG＞BF．
∴AG+BG＞DC，
∴DC＜AB．
故答案为CD∥AB，CD＜AB．

点评：本题考查了全等三角形的判定与性质：判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应角相等，对应边相等．也考查了平行四边形的判定与性质以及三角形三边的关系．