题目内容
 如图,已知△ABC
如图,已知△ABC(1)用尺规作图方法作AC的垂直平分线MN,交AB于点E,交AC于点D,连结CE,(保留作图痕迹,不写作法)
(2)若AD=3,△BCE周长为13,求△ABC的周长.
考点:作图—基本作图,线段垂直平分线的性质
专题:
分析:(1)利用线段垂直平分线的作法作图即可;
(2)根据垂直平分线的性质得到AD=CD,EC=EA,然后根据AD=3求得AC=6,再利用△BCE的周长为13,得到AB+BC=13,从而得到结论.
(2)根据垂直平分线的性质得到AD=CD,EC=EA,然后根据AD=3求得AC=6,再利用△BCE的周长为13,得到AB+BC=13,从而得到结论.
解答:解:(1)如图所示:

(2)∵DE垂直平分AC,
∴AD=CD,EC=EA,
∵AD=3,
∴AC=6,
∵△BCE的周长为13,
∴AB+BC=13,
∴AB+BC+AC=13+6=19.

(2)∵DE垂直平分AC,
∴AD=CD,EC=EA,
∵AD=3,
∴AC=6,
∵△BCE的周长为13,
∴AB+BC=13,
∴AB+BC+AC=13+6=19.
点评:此题主要考查了基本作图,以及线段垂直平分线的作法,等腰三角形的性质,关键是掌握线段垂直平分线的作法.

练习册系列答案
相关题目
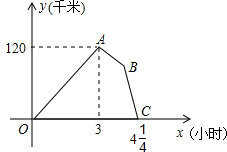 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )| A、快递车从甲地到乙地的速度为100千米/时 | ||
| B、甲、乙两地之间的距离为120千米 | ||
C、图中点B的坐标为(3
| ||
| D、快递车从乙地返回时的速度为90千米/时 |
下列图形,不一定是轴对称图形的是( )
| A、等腰三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=
如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=| k |
| x |
( )
A、y=-
| ||
B、y=-
| ||
C、y=
| ||
D、y=
|
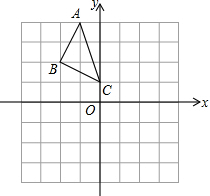 如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:
如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题: 如图,河坝横断面迎水坡AB的坡比为1:
如图,河坝横断面迎水坡AB的坡比为1: