题目内容
15.在分式变形$\frac{-2a(a-x)}{6{x}^{2}(a+x)(a-x)}$=$\frac{a(a+x)}{xM}$中,用a,x的代数式表示M,并写出上述等式成立的条件.分析 根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变.
解答 解:由$\frac{-2a(a-x)}{6{x}^{2}(a+x)(a-x)}$=$\frac{a(a+x)}{xM}$得
分子分母都乘以-(a+x),
$\frac{a(a+x)}{-3{x}^{2}(a+x)^{2}}$=$\frac{a(a+x)}{xM}$.
M=-3x(a+x)2.
上述等式成立的条件是a+x≠0,a-x≠0.
点评 本题考查了分式的性质,分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.A=2a2-3ab+2b2,B=2a2+ab-3b2,则B-A等于( )
| A. | 2ab-5b2 | B. | 4ab+5b2 | C. | -2ab-5b2 | D. | 4ab-5b2 |
20.下列运算结果不正确的有( )
①2a+b=2ab;②4a2-a2=3;③-x2-x2=-2x2;④5mn-5n=m.
①2a+b=2ab;②4a2-a2=3;③-x2-x2=-2x2;④5mn-5n=m.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.某玩具工厂在今年元旦前的某周计划每天生产500个某种品牌的玩具,由于工人实行轮休,每天上班人数不一定相等,实际每天生产个数与计划个数相比情况如表:(增加的个数为正数,减少的个数为负数,其中m,n均为正整数)
根据上述信息,解决下面两个问题:
(1)周五生产了多少个玩具?
(2)这一周实际生产的总个数与该周计划生产的总个数相比,是增加还是减少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | 2m | 2n | -2m | -3n | 2m | -4n | 3n |
(1)周五生产了多少个玩具?
(2)这一周实际生产的总个数与该周计划生产的总个数相比,是增加还是减少?
 已知,在四边形ABCD中,∠BAD=∠D=90°,BM=CM=CD.求证:∠AMC=3∠BAM.
已知,在四边形ABCD中,∠BAD=∠D=90°,BM=CM=CD.求证:∠AMC=3∠BAM.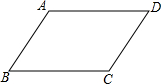 如图,AD∥BC,AD=BC,求证:AB∥DC.
如图,AD∥BC,AD=BC,求证:AB∥DC.