题目内容
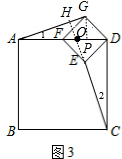
如图,若四边形ABCD、四边形GFED都是正方形,显然图(1)中有AG=CE,AG⊥CE.
(1)当正方形GFED绕D旋转到图(2)和图(3)的位置时,AG、CE满足什么样关系,请写出你的猜想,并对图(3)给予证明.
(2)填空,在图(3)中,当AD=4,DG=
时,则点C到AG的距离为 .
(1)当正方形GFED绕D旋转到图(2)和图(3)的位置时,AG、CE满足什么样关系,请写出你的猜想,并对图(3)给予证明.
(2)填空,在图(3)中,当AD=4,DG=
| 2 |

考点:旋转的性质,全等三角形的判定与性质,正方形的性质
专题:计算题
分析:(1)延长CE交AD于0,交AG于H,根据正方形的性质得AD=CD,DG=DE,∠ADG=∠ADE=45°,则∠CDE=45°,于是可根据“SAS”判定△ADG≌△CDE,得到AG=CE,∠1=∠2,然后根据三角形内角和和得到∠AHO=∠CDO=90°,则CH⊥AG,AG=CE,AG⊥CE;
(2)作GP⊥AD于P,如图3,易得△PDG为等腰直角三角形,得到PD=PG=
DG=1,则AP=AD-PD=3,在Rt△AGP中利用勾股定理可计算出AG=
,接着证明Rt△AGP∽Rt△COD,利用相似比可计算出OC=
,OD=
,所以AO=AD-OD=
,然后证明Rt△AHO∽Rt△CDO,利用相似可计算出OH=
,再利用CH=CO+OH进行计算即可.
(2)作GP⊥AD于P,如图3,易得△PDG为等腰直角三角形,得到PD=PG=
| ||
| 2 |
| 10 |
4
| ||
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
4
| ||
| 15 |
解答:解:(1)AG=CE,AG⊥CE.
证明如下:如图(3),
延长CE交AD于0,交AG于H,
∵四边形ABCD、四边形GFED都是正方形,
∴AD=CD,DG=DE,
而点F在AD上,
∴∠ADG=∠ADE=45°,
∴∠CDE=45°,
在△AGD和△CED中,
,
∴△ADG≌△CDE(SAS),
∴AG=CE,∠1=∠2,
∵∠AOH=∠COD,
∴∠AHO=∠CDO=90°,
∴CH⊥AG,
即AG⊥CE;
(2)作GP⊥AD于P,如图3,
在Rt△DGP中,∵∠GDP=45°,
∴△PDG为等腰直角三角形,
∴PD=PG=
DG=
×
=1,
∴AP=AD-PD=4-1=3,
在Rt△AGP中,AG=
=
,
∵∠1=∠2,
∴Rt△AGP∽Rt△COD,
∴
=
=
,即
=
=
,
∴OC=
,OD=
,
∴AO=AD-OD=4-
=
,
∵∠1=∠2,
∴Rt△AHO∽Rt△CDO,
∴
=
,即
=
,
∴OH=
,
∴CH=CO+OH=
+
=
,
即点C到AG的距离为
.
故答案为
.
证明如下:如图(3),
延长CE交AD于0,交AG于H,
∵四边形ABCD、四边形GFED都是正方形,
∴AD=CD,DG=DE,
而点F在AD上,
∴∠ADG=∠ADE=45°,
∴∠CDE=45°,
在△AGD和△CED中,
|

∴△ADG≌△CDE(SAS),
∴AG=CE,∠1=∠2,
∵∠AOH=∠COD,
∴∠AHO=∠CDO=90°,
∴CH⊥AG,
即AG⊥CE;
(2)作GP⊥AD于P,如图3,
在Rt△DGP中,∵∠GDP=45°,
∴△PDG为等腰直角三角形,
∴PD=PG=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴AP=AD-PD=4-1=3,
在Rt△AGP中,AG=
| PG2+AP2 |
| 10 |
∵∠1=∠2,
∴Rt△AGP∽Rt△COD,
∴
| AG |
| CO |
| PG |
| OD |
| AP |
| CD |
| ||
| OC |
| 1 |
| OD |
| 3 |
| 4 |
∴OC=
4
| ||
| 3 |
| 4 |
| 3 |
∴AO=AD-OD=4-
| 4 |
| 3 |
| 8 |
| 3 |
∵∠1=∠2,
∴Rt△AHO∽Rt△CDO,
∴
| OH |
| OD |
| OA |
| OC |
| OH | ||
|
| ||||
|
∴OH=
4
| ||
| 15 |
∴CH=CO+OH=
4
| ||
| 3 |
4
| ||
| 15 |
8
| ||
| 5 |
即点C到AG的距离为
8
| ||
| 5 |
故答案为
8
| ||
| 5 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了三角形全等的判定与性质、三角形相似的判定与性质和正方形的性质.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
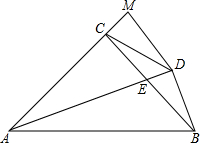 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD.下列结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD.下列结论:①BC+CE=AB;②BD=
| 1 |
| 2 |
其中不正确的结论有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
若a>b,则下列式子正确的是( )
| A、-4a>-4b | ||||
B、
| ||||
| C、4-a>4-b | ||||
| D、a-4>b-4 |
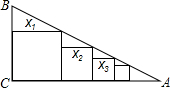 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第2015个正方形的边长为
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第2015个正方形的边长为
 如图所示,直线AB、CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠AOE=50°,求∠COB和∠BOF的大小各为多少?
如图所示,直线AB、CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠AOE=50°,求∠COB和∠BOF的大小各为多少? 如图,将两块直角三角板的直角顶点C叠放在一起.
如图,将两块直角三角板的直角顶点C叠放在一起.