题目内容
 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.考点:平行四边形的判定与性质
专题:证明题
分析:由∠1=∠2,根据平行线的判定,可得BF∥DE,则可得∠AFB=∠ADE,又由∠ABC=∠ADC,BF、DE分别平分∠ABC、∠ADC,可证得∠CBF=∠ADE,即可得∠CBF=∠AFB,则可证得AB∥BC,继而证得结论.
解答:证明:∵∠1=∠2,
∴BF∥DE,
∴∠AFB=∠ADE,
∵BF、DE分别平分∠ABC、∠ADC,
∴∠CBF=
∠ABC,∠ADE=
∠ADC,
∵∠ABC=∠ADC,
∴∠CBF=∠ADE,
∴∠CBF=∠AFB,
∴AD∥BC,
∴∠A+∠ABC=180°,∠C+∠ADC=180°,
∴∠A=∠C.
∴BF∥DE,
∴∠AFB=∠ADE,
∵BF、DE分别平分∠ABC、∠ADC,
∴∠CBF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=∠ADC,
∴∠CBF=∠ADE,
∴∠CBF=∠AFB,
∴AD∥BC,
∴∠A+∠ABC=180°,∠C+∠ADC=180°,
∴∠A=∠C.
点评:此题考查了平行线的判定与性质以及角平分线的定义.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中,正确的是( )
| A、不可能事件在一次实验中也可能发生 |
| B、可能性很小的事件在一次实验中一定发生 |
| C、可能性很大的事件在一次实验中是必然发生 |
| D、可能性很小的事件在一次实验中有可能发生 |
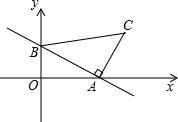 如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°. 如图,直线AB、CD相交于点O,OE⊥AB,OF⊥CD,∠AOC=
如图,直线AB、CD相交于点O,OE⊥AB,OF⊥CD,∠AOC=