题目内容
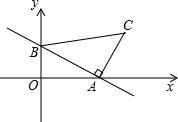 如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.(1)求C点坐标;
(2)在x轴上有一点P,求当PC+PB值最小时,点P的坐标.
考点:全等三角形的判定与性质,一次函数图象上点的坐标特征,轴对称-最短路线问题
专题:
分析:(1)作CD⊥x轴,易证∠OAB=∠ACD,即可证明△ABO≌△CAD,可得AD=OB,CD=OA,即可解题;
(2)作C点关于x轴对称点E,连接BE,即可求得E点坐标,根据点P在直线BE上即可求得点P坐标,即可解题.
(2)作C点关于x轴对称点E,连接BE,即可求得E点坐标,根据点P在直线BE上即可求得点P坐标,即可解题.
解答:解:(1)作CD⊥x轴,
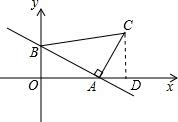
∵∠OAB+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠OAB=∠ACD,
在△ABO和△CAD中,
,
∴△ABO≌△CAD(AAS)
∴AD=OB,CD=OA,
∵y=-x+2与x轴、y轴交于点A、B,
∴A(2,0),B(0,2),
∴点C坐标为(4,2);
(2)作C点关于x轴对称点E,连接BE,
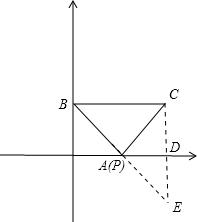
则E点坐标为(4,-2),△ACD≌△AED,
∴AE=AC,
∴直线BE解析式为y=-x+2,
设点P坐标为(x,0),
则(x,0)位于直线BE上,
∴点P坐标为(2,0)于点A重合.

∵∠OAB+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠OAB=∠ACD,
在△ABO和△CAD中,
|
∴△ABO≌△CAD(AAS)
∴AD=OB,CD=OA,
∵y=-x+2与x轴、y轴交于点A、B,
∴A(2,0),B(0,2),
∴点C坐标为(4,2);
(2)作C点关于x轴对称点E,连接BE,

则E点坐标为(4,-2),△ACD≌△AED,
∴AE=AC,
∴直线BE解析式为y=-x+2,
设点P坐标为(x,0),
则(x,0)位于直线BE上,
∴点P坐标为(2,0)于点A重合.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABO≌△CAD是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AD是BC边上的垂直平分线,AD=6,BC=8,E、F是AD上的两点,则图中阴影部分的面积是
如图,在△ABC中,AD是BC边上的垂直平分线,AD=6,BC=8,E、F是AD上的两点,则图中阴影部分的面积是 已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.
已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC、∠ADC,且∠1=∠2,求证:∠A=∠C.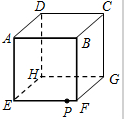 如图所示,是一个边长为60cm的正方体ABCD-EFGH.
如图所示,是一个边长为60cm的正方体ABCD-EFGH. 如图,在四边形ABCD中,AB⊥BC,AD⊥DC,若AB=AD=5cm,BC=4cm,则四边形ABCD的面积为
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,若AB=AD=5cm,BC=4cm,则四边形ABCD的面积为 如图,在四边形ABCD中,已知∠A=135°,∠B=∠D=90°,BC=4,AD=
如图,在四边形ABCD中,已知∠A=135°,∠B=∠D=90°,BC=4,AD=