题目内容
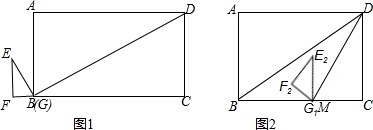
1.如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF=$\sqrt{3}$,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B-M-D方向以每秒$\sqrt{3}$个单位长度平移,得到△E1F1G1,平移过程中,点G1始终在折线B-M-D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,(1)当△E1F1G1的顶点E1恰好在BD上时,t=3秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0<α<180)得到△E2F2G1,点E1、F1分别对应E2、F2,设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
分析 (1)如图1中,连接AC交BD于点O,作OH⊥BC于点H,当△E1F1G1的顶点E1恰好在BD上时,点E平移到点O处.由此即可解决问题.
(2)分三种情形讨论①如图2中,当0<t≤4时,重叠部分是四边形NF1GH,根据S=${S}_{△{E}_{1}{F}_{1}G}$-${S}_{△HN{E}_{1}}$计算.②如图3中,当4<t≤7时,重叠部分是四边形GHNF1,
根据S=${S}_{△G{E}_{1}{F}_{1}}$-${S}_{△HN{E}_{1}}$计算.③如图4中,当7<t≤8时,重叠部分是△GHN.
(3)存在.①如图5中,当∠DQP=90°时,此时只要证明四边形MCQF2是矩形即可.②如图6中,当∠DPQ=90°时,点P与点F2重合,点E、Q、C重合,此时α=120°,DQ=CD=6.
解答 解:(1)如图1中,连接AC交BD于点O,作OH⊥BC于点H.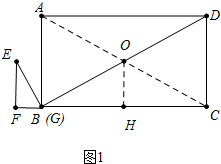
∵四边形ABCD是矩形,
∴AB=CD=6,BO=OD,
∴BH=HC,
∴OH=$\frac{1}{2}$CD=3,
在Rt△DBC中,∵CD=6,∠DBC=30°,
∴BC=6$\sqrt{3}$,BD=12,BH=HC=3$\sqrt{3}$
∵在△EFG中,∠F=90°,GF=$\sqrt{3}$,∠E=30°,
∴EF=3,EB=2$\sqrt{3}$,
∴当△E1F1G1的顶点E1恰好在BD上时,点E平移到点O处.
此时t=$\frac{3\sqrt{3}}{\sqrt{3}}$=3,
∴t=3时,△E1F1G1的顶点E1恰好在BD上,
故答案为3.
(2)在Rt△DCM中,∵∠C=90°,CD=6,∠CDM=30°,
∴CM=2$\sqrt{3}$,DM=4$\sqrt{3}$,
∴BM=4$\sqrt{3}$.
①如图2中,当0<t≤4时,重叠部分是四边形NF1GH,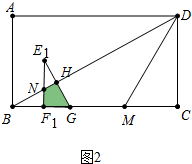
S=${S}_{△{E}_{1}{F}_{1}G}$-${S}_{△HN{E}_{1}}$=$\frac{1}{2}$×$3×\sqrt{3}$-$\frac{1}{2}$•(2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t)(2-$\frac{1}{2}$t)=-$\frac{\sqrt{3}}{4}$t2+2$\sqrt{3}$t-$\frac{5}{2}$$\sqrt{3}$.
②如图3中,当4<t≤7时,重叠部分是四边形GHNF1,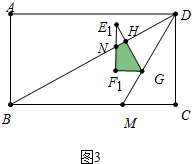
S=${S}_{△G{E}_{1}{F}_{1}}$-${S}_{△HN{E}_{1}}$=$\frac{3\sqrt{3}}{2}$-$\frac{1}{2}$•[2$\sqrt{3}$-$\frac{1}{2}$(8$\sqrt{3}$-$\sqrt{3}$t)]•[2-$\frac{1}{2}$(8-t)]=-$\frac{\sqrt{3}}{8}$t2+$\sqrt{3}$t-$\frac{\sqrt{3}}{2}$.
③如图4中,当7<t≤8时,重叠部分是△GHN,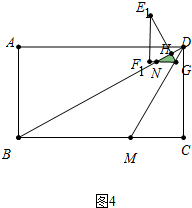
S=$\frac{1}{2}$•$\frac{1}{2}$(8$\sqrt{3}$-$\sqrt{3}$t)•$\frac{\sqrt{3}}{2}$(8$\sqrt{3}$-$\sqrt{3}$t)=$\frac{3\sqrt{3}}{8}$t2-6$\sqrt{3}$t+24$\sqrt{3}$,
综上所述,S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{4}{t}^{2}+2\sqrt{3}t-\frac{5}{2}\sqrt{3}}&{(0<t≤4)}\\{-\frac{\sqrt{3}}{8}{t}^{2}+\sqrt{3}t-\frac{\sqrt{3}}{2}}&{(4<t≤7)}\\{\frac{3\sqrt{3}}{8}{t}^{2}-6\sqrt{3}t+24\sqrt{3}}&{(7<t≤8)}\end{array}\right.$.
(3)存在.
理由:①如图5中,当∠DQP=90°时,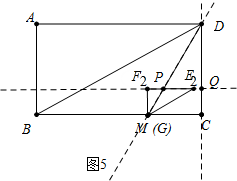
∵∠QCM=∠CQF2=∠QF2M=90°,
∴四边形MCQF2是矩形,
∴CQ=MF2=$\sqrt{3}$,∠F2MC=90°
∴α=90°,DQ=CD-CQ=6=$\sqrt{3}$.
②如图6中,当∠DPQ=90°时,点P与点F2重合,点E、Q、C重合,此时α=120°,DQ=CD=6.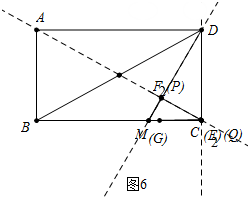
综上所述,当α=90°,DQ=6-$\sqrt{3}$或α=120°,DQ=6时,△DPQ为直角三角形.
点评 本题考查四边形综合题、平移变换、旋转变换、多边形的面积等知识,解题的关键是学会讨论讨论,确定分段函数的自变量的取值范围是难点,学会画好图形解决问题,属于中考压轴题.

 科学实验活动册系列答案
科学实验活动册系列答案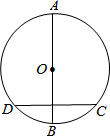 如图⊙O,AB是它的直径,DC是它上面的一条弦,已知DC=6,AB⊥DC,圆心O到DC的距离为4,则圆的半径是( )
如图⊙O,AB是它的直径,DC是它上面的一条弦,已知DC=6,AB⊥DC,圆心O到DC的距离为4,则圆的半径是( )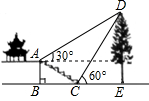 某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.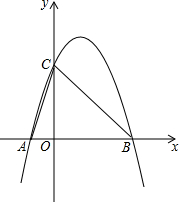 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6