题目内容
已知一元二次方程ax2+bx+c=0的两根为x1=2,x2=-3,则二次三项式ax2+bx+c可分解因式为 .
考点:解一元二次方程-因式分解法
专题:计算题
分析:根据因式分解法解方程,以2和-3为根的一元二次方程为a(x-2)(x+3)=0,于是可得二次三项式ax2+bx+c分解为a(x-2)(x+3).
解答:解:∵一元二次方程ax2+bx+c=0的两根为x1=2,x2=-3,
∴原方程为a(x-2)(x+3)=0,
∴二次三项式ax2+bx+c=a(x-2)(x+3).
故答案为a(x-2)(x+3).
∴原方程为a(x-2)(x+3)=0,
∴二次三项式ax2+bx+c=a(x-2)(x+3).
故答案为a(x-2)(x+3).
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
某服装店把原价为100元的衣服提价10%后,再降价10%销售,则该衣服的价格为( )
| A、100元 | B、1元 |
| C、50元 | D、99元 |
下列说法中错误的是( )
| A、0的相反数是0 |
| B、-2和+2互为相反数 |
| C、符号相反的数互为相反数 |
| D、一个数的绝对值越大,表示它的点在数轴上离原点越远 |
 已知数轴上两点AB对应的数分别是-2,6,数轴上一动点P对应的数为x.
已知数轴上两点AB对应的数分别是-2,6,数轴上一动点P对应的数为x.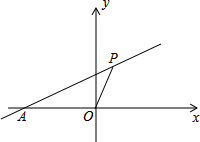 已知如图,点A是x轴负半轴上一点,直线AP,OP交于点P(2,m),直线PA交y轴于点C(0,2),S△AOP=6.
已知如图,点A是x轴负半轴上一点,直线AP,OP交于点P(2,m),直线PA交y轴于点C(0,2),S△AOP=6. 如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为
如图,在三角形ABC中,BC=10cm,若A点到BC的距离AF=8cm,则三角形ABC的面积为