题目内容
 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为
| 5 |
考点:切线的判定
专题:几何图形问题
分析:(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,所以∠APO=∠CBP,而∠A=∠OBA,所以∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(
)2+x2=(x+1)2,然后解方程即可.
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(
| 5 |
解答:(1)证明:连接OB,如图,
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,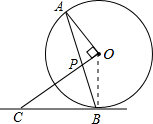
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=
,OC=CP+OP=x+1,
∵OB2+BC2=OC2,
∴(
)2+x2=(x+1)2,
解得x=2,
即BC的长为2.
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,

∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=
| 5 |
∵OB2+BC2=OC2,
∴(
| 5 |
解得x=2,
即BC的长为2.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理.

练习册系列答案
相关题目
下列二次根式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
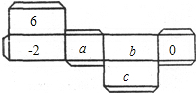 如图是一个长方体墨水瓶纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数.
如图是一个长方体墨水瓶纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数. 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD.
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD. 画出函数y=-x+1的图象,结合图象,回答下列问题.
画出函数y=-x+1的图象,结合图象,回答下列问题. 如图,AE∥BF,AC平分∠BAE,交BF于点C,若∠ACF=130°,则∠B的度数为
如图,AE∥BF,AC平分∠BAE,交BF于点C,若∠ACF=130°,则∠B的度数为