题目内容
4.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变量和对应函数值如表:| x | … | -1 | 0 | 2 | 4 | … |
| y1 | … | 0 | 1 | 3 | 5 | … |
| x | … | -1 | 1 | 3 | 4 | … |
| y2 | … | 0 | -4 | 0 | 5 | … |
| A. | x<-1 | B. | x>4 | C. | -1<x<4 | D. | x<-1或x>4 |
分析 方法一:先在表格中找出点,用待定系数法求出直线和抛物线的解析式,用y2>y1建立不等式,求解不等式即可.
方法二:直接由表得出两函数图象的交点坐标(-1,0),(4,5),再结合变化规律得出结论.
解答 解法一:由表可知,(-1,0),(0,1)在一次函数y1=kx+m的图象上,
∴$\left\{\begin{array}{l}{-k+m=0}\\{m=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{m=1}\end{array}\right.$
∴一次函数y1=x+1,
由表可知,(-1,0),(1,-4),(3,0)在二次函数y2=ax2+bx+c(a≠0)的图象上,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{a+b+c=-4}\\{9a+3b+c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$
∴二次函数y2=x2-2x-3
当y2>y1时,
∴x2-2x-3>x+1,
∴(x-4)(x+1)>0,
∴x>4或x<-1,
故选D,
解法二:如图,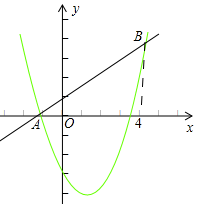
由表得出两函数图象的交点坐标(-1,0),(4,5),
∴x>4或x<-1,
故选D.
点评 此题是二次函数和不等式题目,主要考查了待定系数法,解不等式,解本题的关键是求出直线和抛物线的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.用代数式表示“m的2倍与n平方的差”,正确的是( )
| A. | (2m-n)2 | B. | 2(m-n)2 | C. | 2m-n2 | D. | (m-2n)2 |
19.下列七个数中:0,32,(-5)2,-4,9,π,3-2,有平方根的数的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9.如果a的相反数是-$\frac{2}{3}$,那么a的倒数是( )
| A. | $\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
16.为检测某班40名学生的近视情况,从中抽取了5名学生进行检测,在这个问题中,总体是( )
| A. | 40名学生 | B. | 40名学生的视力结果 | ||
| C. | 5名学生 | D. | 5名学生的视力结果 |
 如图,直线y=kx+b与x轴y轴分别交于点E(-8,0),F(0,6),点A的坐标为(-6,0)
如图,直线y=kx+b与x轴y轴分别交于点E(-8,0),F(0,6),点A的坐标为(-6,0) 用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体需要小正方体最多几块?最少几块?
用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体需要小正方体最多几块?最少几块?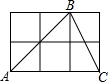 如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为3.
如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为3.