题目内容
3.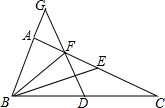 如图所示,在△ABC中,点D是BC的中点,E、F是AC上的点,CE=AB,AF=EF,DF的延长线与BA的延长线相交于点G,求证:AG=AF.
如图所示,在△ABC中,点D是BC的中点,E、F是AC上的点,CE=AB,AF=EF,DF的延长线与BA的延长线相交于点G,求证:AG=AF.
分析 取BE的中点,连接DH、FH,证出HF是△ABE的中位线,HD是△BCE的中位线,由三角形中位线定理得出HF∥AB,HF=$\frac{1}{2}$AB,HD∥CE,HD=$\frac{1}{2}$CE,得出∠G=∠HFD,∠HDF=∠DFC,证出HF=HD,得出∠HFD=∠HDF,再由对顶角相等得出∠G=∠AFG,即可得出AG=AF.
解答 证明:取BE的中点,连接DH、FH,如图所示: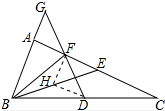
∵AF=EF,点D是BC的中点,
∴HF是△ABE的中位线,HD是△BCE的中位线,
∴HF∥AB,HF=$\frac{1}{2}$AB,HD∥CE,HD=$\frac{1}{2}$CE,
∴∠G=∠HFD,∠HDF=∠DFC,
∵AB=CE,
∴HF=HD,
∴∠HFD=∠HDF,
∵∠AFG=∠DFC,
∴∠G=∠AFG,
∴AG=AF.
点评 本题考查了三角形中位线定理、等腰三角形的判定与性质、对顶角相等等知识;本题综合性强,有一定难度.

练习册系列答案
相关题目
8.把图形M先向左平移2个单位,再向上平移6个单位,如果平移后的图形上有一点A的坐标为(-3,3),那么平移前该点的坐标为( )
| A. | (-1,-3) | B. | (-5,9) | C. | (-1,9) | D. | (-5,3) |
 已知:在△ABC中,AB=AC=8cm,BC=6cm,∠A=n°,AB的垂直平分线分别交AB于点D,交AC于E.求:
已知:在△ABC中,AB=AC=8cm,BC=6cm,∠A=n°,AB的垂直平分线分别交AB于点D,交AC于E.求: 如图,在△ABC中,∠C=90°,AC=BC,AD是角平分线,DE⊥AB.垂足为E.求证:BE=DE=CD.
如图,在△ABC中,∠C=90°,AC=BC,AD是角平分线,DE⊥AB.垂足为E.求证:BE=DE=CD.