题目内容
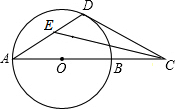 如图,AB是圆O的直径,C是AB延长线上的一点,CD是圆O的切线,切点为D,CE平分∠ACD,交AD于点E,求∠DEC的度数.
如图,AB是圆O的直径,C是AB延长线上的一点,CD是圆O的切线,切点为D,CE平分∠ACD,交AD于点E,求∠DEC的度数.考点:切线的性质
专题:
分析:连结OD,BD,根据切线的性质得OD⊥CD,则∠4+∠ODB=90°,而AB为⊙O的直径,得到∠ADB=90°,得∠A+∠ABD=90°,得到∠A=∠4,又∠3=∠A+∠2,∠5=∠1+∠4,可得∠3=∠5,得到∠3=
×90°=45°.
| 1 |
| 2 |
解答: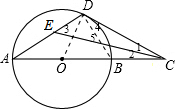 解:如图,连结OD,BD.
解:如图,连结OD,BD.
∵CD为⊙O的切线,
∴OD⊥CD,
∴∠4+∠ODB=90°,
而AB为⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
而∠ABD=∠ODB,
∴∠A=∠4,
又∵∠3=∠A+∠2,
∠5=∠1+∠4,
而EC平分∠ACD,即∠1=∠2,
∴∠3=∠5,
∴∠3=
×90°=45°.
 解:如图,连结OD,BD.
解:如图,连结OD,BD.∵CD为⊙O的切线,
∴OD⊥CD,
∴∠4+∠ODB=90°,
而AB为⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
而∠ABD=∠ODB,
∴∠A=∠4,
又∵∠3=∠A+∠2,
∠5=∠1+∠4,
而EC平分∠ACD,即∠1=∠2,
∴∠3=∠5,
∴∠3=
| 1 |
| 2 |
点评:本题考查了切线的性质:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等.也考查了直径所对的圆周角为直角以及三角形外角的性质.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

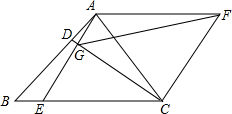 如图,△ABC和△ACF均为等边三角形,点D、E分别为AD,BE边上的点,且AD=BE,AE与CD交于G点,连接GF.
如图,△ABC和△ACF均为等边三角形,点D、E分别为AD,BE边上的点,且AD=BE,AE与CD交于G点,连接GF. 如图,已知△ABC为等边三角形,O为其内部一点,将△AOC绕点A旋转60°得到△ADB,连接OD,DB,已知AO=3cm,BO=5cm,CO=4cm,求△ODB的周长.
如图,已知△ABC为等边三角形,O为其内部一点,将△AOC绕点A旋转60°得到△ADB,连接OD,DB,已知AO=3cm,BO=5cm,CO=4cm,求△ODB的周长.