题目内容
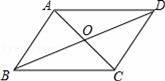
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )


A.1对 B.2对 C.3对 D.4对
D【分析】平行四边形的性质是:对边相互平行且相等,对角线互相平分.这样不难得出:AD=BC,AB=CD,AO=CO,DO=BO,再利用“对顶角相等”就很容易找到全等的三角形:△ACD≌△CAB(SSS),△ABD≌△CDB(SSS),△AOD≌△COB(SAS),△AOB≌△COD(SAS).
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中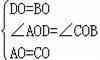

∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中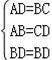
 ,
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.

【点评】考查了平行四边形的性质和全等三角形的判定,三角形全等的条件有时候是直接给的,有时候是根据已知条件推出的,还有时是由已知图形的性质得出的,做题时要全面考虑.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目





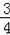
 的图象c交x轴于A,B两点(A在B的左侧),过A点的直线
的图象c交x轴于A,B两点(A在B的左侧),过A点的直线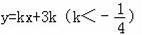
 交c于另一点C(x1,y1),交y轴于M.
交c于另一点C(x1,y1),交y轴于M.
 )且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;
)且Q点是直线AC上的一个动点.求出当△DBQ与△AOM相似时点Q的坐标;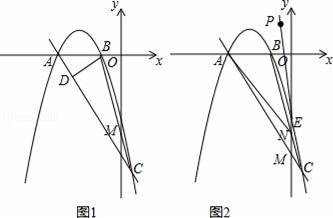


 =0的两根,若实数a满足a+x1+x2﹣x1•x2=2018,则a= .
=0的两根,若实数a满足a+x1+x2﹣x1•x2=2018,则a= .
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) ;
;