题目内容

16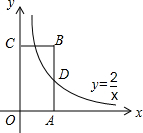．如图，反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为（　　）
A．2B．4C．5D．8

分析 由反比例函数的系数k的几何意义可知：OA•AD=2，然后可求得OA•AB的值，从而可求得矩形OABC的面积．

解答 解：∵y=$\frac{2}{x}$，
∴OA•AD=2．
∵D是AB的中点，
∴AB=2AD．
∴矩形的面积=OA•AB=2AD•OA=2×2=4．
故选：B．

点评 本题主要考查的是反比例函数k的几何意义，掌握反比例函数系数k的几何意义是解题的关键．

练习册系列答案
相关题目
6．某校想了解本校学生每周的课外阅读时间情况，随机抽取了八年级部分学生，对学生每周的课外阅读时间x（单位：h）进行分组整理，并绘制了如图所示的不完整的统计图；请根据图中提供的信息，回答下列问题：
（1）a=10%，并写出该扇形所对的圆心角的度数为36°，请补全条形图．
（2）在这次抽样调查中，课外阅读时间的众数和中位数分别是多少？
（3）如果该校共有学生2000人，请你估计该校“课外阅读时间不少于7h”的学生人数大约有多少人？
7．解决下列问题：
甲、乙两所学校的同学一起去北京农业职业学院参加学农教育实践活动，活动结束时，两校各派出一些志愿者协助老师布置闭营成果展示会活动现场．老师先派了9名甲校志愿者搬运物品，发现此时剩下的甲校志愿者是乙校志愿者的一半，根据需要又派了14名乙校志愿者也去搬运，这时剩下的甲校志愿者比剩下的乙校志愿者少7人．问：甲、乙两所学校各有志愿者多少人？
4．单项式$\frac{π{r}^{2}}{2}$的系数是（　　）
A．$\frac{1}{2}$B．πC．2D．$\frac{π}{2}$
11．计算-42的结果等于（　　）
A．-8B．-16C．16D．8
1．如图，直线AB∥CD，OG是∠EOB的平分线，∠EFD=70°，则∠BOG的度数是（　　）
A．70°B．20°C．35°D．40°
8．2016年欧洲杯足球赛中，某国家足球队首发上场的11名队员身高如表：
 身高（cm）176 178 180 182 186 188 192 
 人数 1 2 3 2 1 1 1
则这11名队员身高的众数和中位数分别是（　　）（单位：cm）
A．180，182B．180，180C．182，182D．3，2
5．方程组$\left\{\begin{array}{l}{x-y+z=0}\\{2x+3y-z=3}\\{x-2y-z=-2}\end{array}\right.$，消去未知数x后得到的二元一次方程组是$\left\{\begin{array}{l}{5y-3z=3}\\{y+2z=2}\end{array}\right.$．
6．把方程x+4y=5化成用含x的代数式表示y的形式为y=$\frac{5-x}{4}$，化成用含y的代数式表示x的形式为x=5-4y．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网