题目内容
已知直线y=kx+b经过点(0,6),且平行于直线y=-2x.
(1)求该直线的函数解析式;
(2)如果这条直线经过点P(m,4),求m的值.
(1)求该直线的函数解析式;
(2)如果这条直线经过点P(m,4),求m的值.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)先根据两直线平行的问题得到k=-2,然后把(0,6)代入y=-2x+b中求出b的值,从而得到该直线的函数解析式;
(2)根据一次函数图象上点的坐标特征,把P(m,4)代入y=-2x+6中可求出m的值.
(2)根据一次函数图象上点的坐标特征,把P(m,4)代入y=-2x+6中可求出m的值.
解答:解:(1)∵直线y=kx+b平行于直线y=-2x,
∴k=-2,
把(0,6)代入y=-2x+b得b=6,
∴该直线的函数解析式为y=-2x+6;
(2)把P(m,4)代入y=-2x+6得-2m+4=6,
解得m=-1.
∴k=-2,
把(0,6)代入y=-2x+b得b=6,
∴该直线的函数解析式为y=-2x+6;
(2)把P(m,4)代入y=-2x+6得-2m+4=6,
解得m=-1.
点评:本题考查了两条直线相交或平行的问题两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
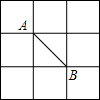 如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )
如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )| A、5个 | B、6个 | C、7个 | D、8个 |
在阳光下摆弄一个矩形,它的影子不可能是( )
| A、线段 | B、矩形 |
| C、等腰梯形 | D、平行四边形 |
如果两个相似三角形的面积比是1:2,那么它们的周长比是( )
| A、1:4 | ||
B、1:
| ||
C、
| ||
| D、4:1 |
 如图,∠AOD=150°,∠AOB=40°,∠COD=70°,OM、ON分别是∠AOB、∠COD的平分线,求∠MON的度数.
如图,∠AOD=150°,∠AOB=40°,∠COD=70°,OM、ON分别是∠AOB、∠COD的平分线,求∠MON的度数. 如图所示,已知线段AB=12cm,点O是AB上一点,C为AO的中点,点D在线段OB上,且AO:OD:DB=3:2:1,求线段AC的长.
如图所示,已知线段AB=12cm,点O是AB上一点,C为AO的中点,点D在线段OB上,且AO:OD:DB=3:2:1,求线段AC的长. 如图,是一个立方体纸盒的平面展开图,其中“有志不在年高”6个字分别写在这个立方体的6个面上,那么,原立方体中“有”的对面是( )
如图,是一个立方体纸盒的平面展开图,其中“有志不在年高”6个字分别写在这个立方体的6个面上,那么,原立方体中“有”的对面是( ) 如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是
如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是