ЬтФПФкШн
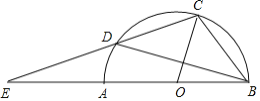
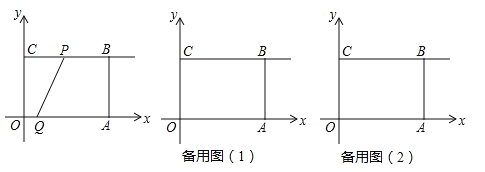
ЁОЬтФПЁПвбжЊЕуAЃЌBЗжБ№дкxжсКЭyжсЩЯЃЌЧв![]() ЃЌЕуCЕФзјБъЪЧ
ЃЌЕуCЕФзјБъЪЧ![]() ЃЌABгыOCЯрНЛгкЕуGЃЎЕуPДгOГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШДгOдЫЖЏЕНCЃЌЙ§PзїжБЯп
ЃЌABгыOCЯрНЛгкЕуGЃЎЕуPДгOГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШДгOдЫЖЏЕНCЃЌЙ§PзїжБЯп![]() ЗжБ№НЛOAЃЌOBЛђACЃЌBCгкEЃЌFЃЎНтД№ЯТСаЮЪЬтЃК
ЗжБ№НЛOAЃЌOBЛђACЃЌBCгкEЃЌFЃЎНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉжБНгаДГіЕуGЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуPдЫЖЏЕФЪБМфЮЊtЃЌжБЯпEFдкЫФБпаЮOACBФкЩЈЙ§ЕФУцЛ§ЮЊsЃЌЧыЧѓГіsгыtЕФКЏЪ§ЙиЯЕЪНЃЛВЂЧѓГіЕБtЮЊКЮжЕЪБЃЌжБЯпEFЦНЗжЫФБпаЮOACBЕФУцЛ§ЃЛ
ЃЈ3ЃЉЩшЯпЖЮOCЕФжаЕуЮЊQЃЌPдЫЖЏЕФЪБМфЮЊtЃЌЧѓЕБtЮЊКЮжЕЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЎ
ЮЊжБНЧШ§НЧаЮЃЎ
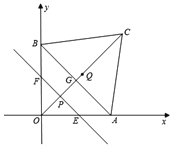
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ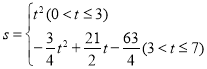 ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌжБЯпEFЦНЗжЫФБпаЮOABCЕФУцЛ§ЃЛЃЈ3ЃЉЕБ
ЪБЃЌжБЯпEFЦНЗжЫФБпаЮOABCЕФУцЛ§ЃЛЃЈ3ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЎ
ЮЊжБНЧШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌвдМА
ЃЌвдМА![]() ЕуКсзјБъЯрЕШЕУГі
ЕуКсзјБъЯрЕШЕУГі![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() жаЕуЃЌМДПЩЕУГіД№АИЃЛ
жаЕуЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉЗжБ№ИљОнЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЕУГі
ЪБЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЕУГі![]() гы
гы![]() ЕФЙиЯЕЪБМДПЩЃЛ
ЕФЙиЯЕЪБМДПЩЃЛ
ЃЈ3ЃЉРћгУЂйЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЪБЃЌвдМАЂкЕБ
ЪБЃЌвдМАЂкЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЪБЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЕУГіМДПЩ.
ЪБЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЕУГіМДПЩ.
ЃЈ1ЃЉGЕуЕФзјБъЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпCЕФзјБъЪЧ![]() ЃЌ
ЃЌ
ЁрOCЪЧ![]() ЕФНЧЦНЗжЯпЃЌ
ЕФНЧЦНЗжЯпЃЌ ЃЎ
ЃЎ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
![]()
![]() ЃЌ
ЃЌ
ЁрsгыtЕФКЏЪ§ЙиЯЕЪНЪЧЃК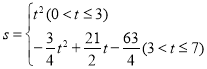
ЕБжБЯпEFЦНЗжЫФБпаЮOABCЕФУцЛ§ЪБгаЃК![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЈВЛЗћКЯЬтвтЩсШЅЃЉЃЌ
ЃЈВЛЗћКЯЬтвтЩсШЅЃЉЃЌ![]() ЃЌ
ЃЌ
ЙЪЕБ![]() ЪБЃЌжБЯпEFЦНЗжЫФБпаЮOABCЕФУцЛ§ЃЛ
ЪБЃЌжБЯпEFЦНЗжЫФБпаЮOABCЕФУцЛ§ЃЛ
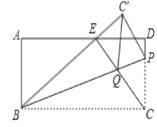
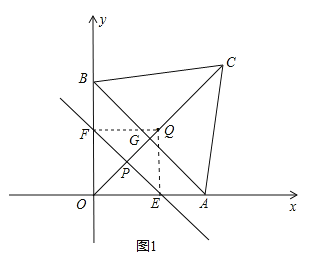
ЃЈ3ЃЉЂйШчЭМ1ЃЌЕБPдкЯпЖЮOQЩЯЃЌЧв![]() ЪБЃЌ
ЪБЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЫФБпаЮOEQFЪЧе§ЗНаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЛ
ЮЊжБНЧШ§НЧаЮЃЛ
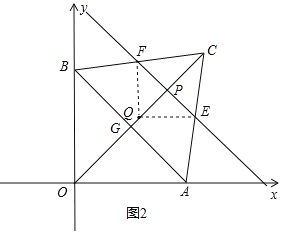
ЂкШчЭМ2ЃЌЕБPдкЯпЖЮCQЩЯЃЌЧв![]() ЪБЃЌ
ЪБЃЌ
ЭЌРэПЩжЄЃК![]() ЃЌ
ЃЌ
Ёр![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
МД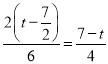 ЃЎ
ЃЎ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪЕБ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊжБНЧШ§НЧаЮ
ЮЊжБНЧШ§НЧаЮ