题目内容
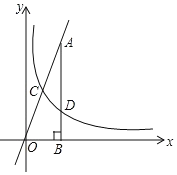
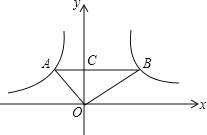
【题目】如图,在直角坐标系中,O为坐标原点,函数![]() 和
和![]() 的图象上,分别有A.B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=
的图象上,分别有A.B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,则线段AB的长度为( )
,则线段AB的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据反比例函数k的几何意义得到![]() |k1|=
|k1|=![]() ,
,![]() |k2|=
|k2|=![]() ,解得k1=-1,k2=9,设C点坐标为(0,t),则A点坐标为(-
,解得k1=-1,k2=9,设C点坐标为(0,t),则A点坐标为(-![]() ,t),B点坐标为(
,t),B点坐标为(![]() ,t),再证明Rt△AOC∽Rt△OBC,利用相似比得到t:
,t),再证明Rt△AOC∽Rt△OBC,利用相似比得到t:![]() =
=![]() :t,解得t=
:t,解得t=![]() ,然后计算AB=
,然后计算AB=![]() +
+![]() 即可.
即可.
∵AB∥x轴,交y轴于点C,
∴S△AOC=![]() |k1|=
|k1|=![]() ,S△BOC=
,S△BOC=![]() |k2|=
|k2|=![]() ,
,
∴k1=-1,k2=9,
设C点坐标为(0,t),则A点坐标为(-![]() ,t),B点坐标为(
,t),B点坐标为(![]() ,t),
,t),
∵OA⊥OB,
∴∠AOC+∠BOC=90°,
而∠AOC+∠OAC=90°,
∴∠OAC=∠BOC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:![]() =
=![]() :t,解得t=
:t,解得t=![]() ,
,
∴AB=![]() +
+![]() =
=![]() .
.
故选B.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目