题目内容
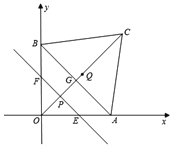
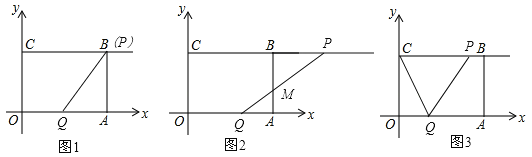
【题目】已知:如图所示,在平面直角坐标系xoy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动.设点P、点Q的运动时间为t(s).
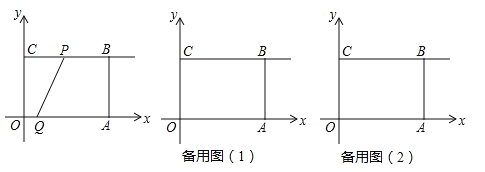
(1)当t=1s时,求经过点O,P,A三点的抛物线的解析式;
(2)当t=2s时,求tan∠QPA的值;
(3)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(4)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)t=3s;(4)
;(3)t=3s;(4)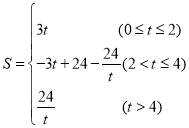 .
.
【解析】
(1)可求得P点坐标,由O、P、A的坐标,利用待定系数法可求得抛物线解析式;
(2)当t=2s时,可知P与点B重合,在Rt△ABQ中可求得tan∠QPA的值;
(3)用t可表示出BP和AQ的长,由△PBM∽△QAM可得到关于t的方程,可求得t的值;
(4)当点Q在线段OA上时,S=S△CPQ;当点Q在线段OA上,且点P在线段CB的延长线上时,由相似三角形的性质可用t表示出AM的长,由S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ,可求得S与t的关系式;当点Q在OA的延长线上时,设CQ交AB于点M,利用△AQM∽△BCM可用t表示出AM,从而可表示出BM,S=S△CBM,可求得答案.
(1)当t=1s时,则CP=2,∵OC=3,四边形OABC是矩形,∴P(2,3),且A(4,0),
∵抛物线过原点O,∴可设抛物线解析式为![]() ,
,
∴![]() ,解得:
,解得: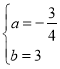 ,
,
∴过O、P、A三点的抛物线的解析式为![]() ;
;
(2)当t=2s时,则CP=2×2=4=BC,即点P与点B重合,OQ=2,如图1,
∴AQ=OA﹣OQ=4﹣2=2,且AP=OC=3,
∴tan∠QPA=![]() =
=![]() ;
;
(3)当线段PQ与线段AB相交于点M,则可知点Q在线段OA上,点P在线段CB的延长线上,如图2,
则CP=2t,OQ=t,∴BP=PC﹣CB=2t﹣4,AQ=OA﹣OQ=4﹣t,
∵PC∥OA,∴△PBM∽△QAM,
∴![]() ,且BM=2AM,
,且BM=2AM,
∴![]() =2,解得t=3,
=2,解得t=3,
∴当线段PQ与线段AB相交于点M,且BM=2AM时,t为3s;
(4)当0≤t≤2时,如图3,由题意可知CP=2t,∴S=S△PCQ=![]() ×2t×3=3t;
×2t×3=3t;
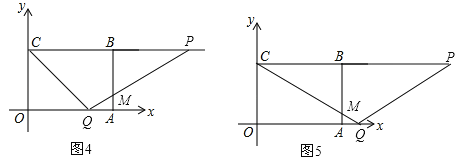
当2<t≤4时,设PQ交AB于点M,
如图4,由题意可知PC=2t,OQ=t,则BP=2t﹣4,AQ=4﹣t,
同(3)可得![]() =
=![]() ,
,
∴BM=![]() AM,∴3﹣AM=
AM,∴3﹣AM=![]() AM,解得AM=
AM,解得AM=![]() ,
,
∴S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ=3×4﹣![]() ×t×3﹣
×t×3﹣![]() ×(4﹣t)×
×(4﹣t)×![]() =24﹣
=24﹣![]() ﹣3t;
﹣3t;
当t>4时,设CQ与AB交于点M,如图5,由题意可知OQ=t,AQ=t﹣4,
∵AB∥OC,∴![]() ,即
,即![]() ,解得AM=
,解得AM=![]() ,
,
∴BM=3﹣![]() =
=![]() ,∴S=S△BCM=
,∴S=S△BCM=![]() ×4×
×4×![]() =
=![]() ;
;
综上可知: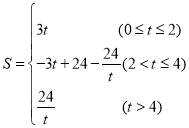 .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.