Question

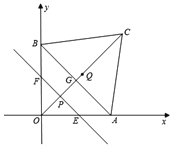
【题目】如图，△ABC内接于⊙O，∠CBG=∠A，CD为直径，OC与AB相交于点E，过点E作EF⊥BC，垂足为F，连接BD．

（1）求证：BG与⊙O相切；

（2）若，求的值．

Answer 1

【答案】(1)见解析 （2）=

【解析】

（1）延长BO交⊙O 于H，连接CH．想办法证明OB⊥BG即可．

（2）利用相似三角形的性质即可解决问题．

（1）证明：延长BO交⊙O 于H，连接CH．

∵BH是直径，

∴∠BCH=90°，

∴∠CBH+∠H=90°，

∵∠CBG=∠CAB=∠H，

∴∠CBG+∠CBH=90°，

∴OB⊥BG，

∴BG是⊙O的切线．

（2）解：连接AD．

∵CD是直径，

∴∠CAD=90°，

∵EF⊥BC，

∴∠BFE=∠CAD=90°，

∵∠FBE=∠CDA，

∴△EBF∽△CDA，

∴=，

∴=，

∴=．