题目内容
11.设ab≠0且b>a,求一次函数y=ax+b、y=bx+a的图象交点的坐标.分析 根据两直线的交点问题,通过解方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=bx+a}\end{array}\right.$即可得到两直线的交点坐标.
解答 解:解方程组$\left\{\begin{array}{l}{y=ax+b}\\{y=bx+a}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=a+b}\end{array}\right.$,
所以一次函数y=ax+b、y=bx+a的图象交点的坐标为(1,a+b).
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
20.把抛物线y=-2(x-1)2+1的图象向左平移3个单位,再向下平移4个单位,所得的抛物线的函数关系式是( )
| A. | y=-2(x+2)2-3 | B. | y=-2(x-4)2-3 | C. | y=2(x+2)2-6D | D. | y=-2(x-4)2+5 |
 如图,Rt△ABC中,∠ACB=90°,分别以AB、BC、CA为直径向外作半圆,面积分别为S1、S2、S3三者的数量关系,并说明理由.
如图,Rt△ABC中,∠ACB=90°,分别以AB、BC、CA为直径向外作半圆,面积分别为S1、S2、S3三者的数量关系,并说明理由.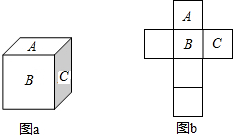 如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.
如图,正方体a的上、前、右三个面上分别注有A,B,C三个字母,它的展开图如图b所示,请用D,E,F,三个字母在展开图上分别标注下、后、左三个面.