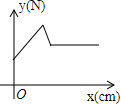题目内容
1.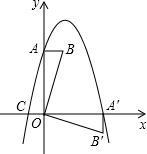 在平面直角坐标系中,O为坐标原点,Rt△ABO如图放置,点A、B的坐标分别为(0,3)、(1,3),将此直角三角形绕点O顺时针旋转90°,得到Rt△A′B′O,若抛物线y=-x2+bx+c过点A,A′,与x轴的另一个交点为C.
在平面直角坐标系中,O为坐标原点,Rt△ABO如图放置,点A、B的坐标分别为(0,3)、(1,3),将此直角三角形绕点O顺时针旋转90°,得到Rt△A′B′O,若抛物线y=-x2+bx+c过点A,A′,与x轴的另一个交点为C.(1)求点C的坐标;
(2)设抛物线的顶点为D,过点D作直线DM⊥x轴于M,P为线段BM上一动点,求以A,B,P为顶点的三角形和以C,P,M为顶点的三角形相似时点P的坐标;
(3)在抛物线上是否存在点E,使得△AA′D和△AA′E的面积相等?若存在,请求出点E的坐标;若不存在,请说明理由.
分析 (1)根据旋转的性质易得点A'的坐标为(3,0),再把A (0,3),A'(3,0)代入y=-x2+bx+c中得到关于b、c的方程组,解方程组求出b、c可得抛物线的解析式为y=-x2+2x+3,然后计算函数值为0时的自变量得值即可得到C(-1,0);
(2)如图1,先利用抛物线的性质得到顶点D的坐标为(1,4),抛物线的对称轴为直线x=1,则可判断点B在直线DM上,设点P的坐标为(1,y),然后分类讨论:当△ABP∽△CMP时,利用相似比得$\frac{1}{2}$=$\frac{3-y}{y}$;
当△ABP∽△PMC时,利用相似比得$\frac{1}{y}$=$\frac{3-y}{2}$,再分别解方程求出y即可得到满足条件的P点坐标;
(3)如图2,易得直线AA'的解析式为y=-x+3,利用三角形面积公式,利用△AA′D和△AA′E的面积相等可判断直线DE∥AA′,则可设直线DE的解析式为y=-x+q,接着把D(1,4)代入求出q得到直线DE的解析式为y=-x+5,则直线y=-x+5与y轴的交点F的坐标为(0,5),于是通过解方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=-{x}^{2}+2x+3}\end{array}\right.$可得E点坐标为(2,3);然后把直线AA′向下平移2个单位所得直线解析式为y=-x+1,所以直线y=-x+1到直线AA′的距离等于直线DE到AA′的距离,设直线y=-x+1于抛物线交于点E′和E″,利用三角形面积公式可判断△AA′D、△AA′E′、△AA′E″的面积都相等,则可通过解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$可确定此时E点坐标.
解答 解:(1)∵Rt△A'B'O由Rt△ABO旋转得到,点A的坐标为(0,3),
∴点A'的坐标为(3,0),
∵抛物线y=-x2+bx+c过A (0,3),A'(3,0),
∴$\left\{\begin{array}{l}c=3\\-9+3b+c=0\end{array}\right.$,解得$\left\{\begin{array}{l}b=2\\ c=3\end{array}\right.$,
∴过点A,A'的抛物线的解析式为y=-x2+2x+3,
令y=0,-x2+2x+3=0,解得x1=-1,x2=3,
∴C(-1,0);
(2)如图1,y=-x2+2x+3=-(x-1)2+4,则顶点D的坐标为(1,4),抛物线的对称轴为直线x=1,
∴点B在直线DM上,
设点P的坐标为(1,y),则AB=1,CM=2,PM=y,BP=3-y,
当△ABP∽△CMP时,$\frac{AB}{CM}$=$\frac{BP}{MP}$,即$\frac{1}{2}$=$\frac{3-y}{y}$,解得y=2,此时P点坐标为(1,2);
当△ABP∽△PMC时,$\frac{AB}{PM}$=$\frac{PB}{CM}$,即$\frac{1}{y}$=$\frac{3-y}{2}$,
整理得y2-3y+2=0,解得y1=1,y2=2,此时P点坐标为(1,1)或(1,2),
综上所述,满足条件的P点坐标为(1,1)或(1,2);
(3)存在.
如图2,易得直线AA'的解析式为y=-x+3,
∵△AA′D和△AA′E的面积相等,
∴直线DE∥AA′,
设直线DE的解析式为y=-x+q,
把D(1,4)代入得-1+q=4,解得q=5,
∴直线DE的解析式为y=-x+5,
则直线y=-x+5与y轴的交点F的坐标为(0,5),
解方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=-{x}^{2}+2x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,此时E点坐标为(2,3);
∵AF=5-3=2,
∴把直线AA′向下平移2个单位所得直线解析式为y=-x+1,直线y=-x+1到直线AA′的距离等于直线DE到AA′的距离,
设直线y=-x+1于抛物线交于点E′和E″,此时△AA′D、△AA′E′、△AA′E″的面积都相等,
解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{3+\sqrt{17}}{2}}\\{y=\frac{-1-\sqrt{17}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{17}}{2}}\\{y=\frac{-1+\sqrt{17}}{2}}\end{array}\right.$,此时E点坐标为($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$)或($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$);
综上所述,E点坐标为(2,3)或($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$)或($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$).
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、旋转的性质和相似三角形的性质;能利用待定系数法求函数解析式,会求抛物线与一次函数的交点坐标;理解坐标与图形的性质;会灵活运用三角形面积公式.

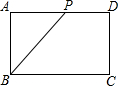 如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )
如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )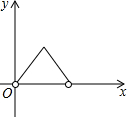
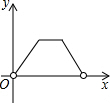
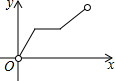
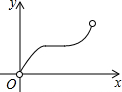
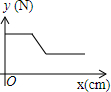
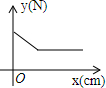
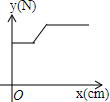
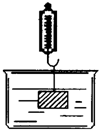 如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )
如图,在物理实验课上,小明用弹簧秤将铁块A从完全置身水槽外,到匀速向下放入盛有水的水槽中,直至铁块完全浸入水面下的一定深度,则图能反映弹簧秤的读数y(单位:N)与铁块下降的高度x(单位:cm)之间的函数关系的大致图象是( )