题目内容
1．甲、乙两人在400米长的环形跑道上练习跑步．他们从同一地点同时出发，沿相同方向跑步，甲的速度为4米/秒，乙的速度为5米/秒，（1）设甲跑x秒后，乙可超过甲一圈，列出以x为未知数的方程；
（2）设甲跑y圈后，乙可超过甲一圈，列出以y为未知数的方程．
分析 （1）根据等量关系：乙跑的路程-甲跑的路程=一圈的长度，由路程=速度×时间，分别得到乙跑的路程，甲跑的路程，依此列出方程求解即可；
（2）根据等量关系：乙跑的时间=甲跑的时间，依此列出方程求解即可．
解答 解：（1）依题意有
5x-4x=400，
解得x=400．
答：甲跑400秒后，乙可超过甲一圈；
（2）依题意有
$\frac{400y}{4}$=$\frac{400（y+1）}{5}$，
解得x=4．
答：甲跑4圈后，乙可超过甲一圈．
点评 考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．
练习册系列答案
相关题目
13．某校举行元旦文娱演出，由参加演出的10个班各推选一名评委，每个节目演出后的得分取各评委给分的平均数，下面是对某班的一个节目各评委给出的评分表：
（1）你对5号和9号评委给出的分有何想法？
（2）10位评委的平均得分是多少？此得分能否反映该节目的水平？
（3）如果去掉一个最高分和去掉一个最低分，再计算平均数应是多少？后一平均数能反映出该节目实际水平吗？
（4）一般情形，如果评委较多，为了使评分能反映实际水平，还可做怎样的改进？
| 评委号数 | 评分 | 评委号数 | 评分 |
| 1 | 7.20 | 6 | 7.30 |
| 2 | 7.25 | 7 | 7.20 |
| 3 | 7.00 | 8 | 7.10 |
| 4 | 7.10 | 9 | 6.20 |
| 5 | 10.00 | 10 | 7.15 |
（2）10位评委的平均得分是多少？此得分能否反映该节目的水平？
（3）如果去掉一个最高分和去掉一个最低分，再计算平均数应是多少？后一平均数能反映出该节目实际水平吗？
（4）一般情形，如果评委较多，为了使评分能反映实际水平，还可做怎样的改进？
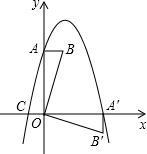在平面直角坐标系中，O为坐标原点，Rt△ABO如图放置，点A、B的坐标分别为（0，3）、（1，3），将此直角三角形绕点O顺时针旋转90°，得到Rt△A′B′O，若抛物线y=-x2+bx+c过点A，A′，与x轴的另一个交点为C．
如图，在正方形ABCD中，AB=12，E是AB边上一点，且AE=3BE，P是对角线AC上一动点，则PB+PE的最小值是15．