题目内容
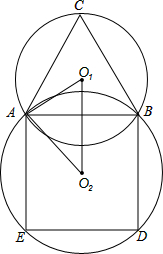 如图所示,⊙O1和⊙O2相交于A、B两点,在⊙O1中,△ABC为正三角形,在⊙O2中四边形ABDE为正方形,若O1A=2,则O2A=
如图所示,⊙O1和⊙O2相交于A、B两点,在⊙O1中,△ABC为正三角形,在⊙O2中四边形ABDE为正方形,若O1A=2,则O2A=考点:圆的综合题,全等三角形的判定与性质,等腰三角形的性质,正多边形和圆,特殊角的三角函数值
专题:计算题
分析:连接O1B、O2B,易证△AO1O2≌△BO1O2,则有∠AO1O2=∠BO1O2,∠AO2O1=∠BO2O1.从而得到O1O2⊥AB,∠AO1O2=60°,∠AO2O1=45°,然后利用三角函数就可解决问题.
解答: 解:连接O1B、O2B,如图所示,
解:连接O1B、O2B,如图所示,
由题可得:∠AO1B=
=120°,∠AO2B=
=90°.
在△AO1O2和△BO1O2中,
.
∴△AO1O2≌△BO1O2.
∴∠AO1O2=∠BO1O2,∠AO2O1=∠BO2O1.
∴O1O2⊥AB,∠AO1O2=60°,∠AO2O1=45°.
在Rt△AO1H中,
AH=AO1•sin∠AO1H=2×
=
.
在Rt△AO2H中,
sin∠AO2H=
=
=
,
解得:AO2=
.
故答案为:
.
 解:连接O1B、O2B,如图所示,
解:连接O1B、O2B,如图所示,由题可得:∠AO1B=
| 360° |
| 3 |
| 360° |
| 4 |
在△AO1O2和△BO1O2中,
|
∴△AO1O2≌△BO1O2.
∴∠AO1O2=∠BO1O2,∠AO2O1=∠BO2O1.
∴O1O2⊥AB,∠AO1O2=60°,∠AO2O1=45°.
在Rt△AO1H中,
AH=AO1•sin∠AO1H=2×
| ||
| 2 |
| 3 |
在Rt△AO2H中,
sin∠AO2H=
| AH |
| AO2 |
| ||
| AO2 |
| ||
| 2 |
解得:AO2=
| 6 |
故答案为:
| 6 |
点评:本题考查了正多边形与圆、全等三角形的判定与性质、等腰三角形的性质、三角函数等知识,而利用三角函数是解决本题的关键.

练习册系列答案
相关题目
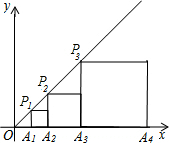 如图,直线l的解析式为y=x+1,点A1(1,0),过A1作x轴的垂线与直线l交于点P1.在线段A1P1右侧,以A1P1为边长作正方形,与x轴交于A2.过A2作x轴的垂线与直线l交于点P2.在线段A2P2右侧,以A2P2长为边长作正方形,与x轴交于A3.按照此法做下去,则P3的坐标为
如图,直线l的解析式为y=x+1,点A1(1,0),过A1作x轴的垂线与直线l交于点P1.在线段A1P1右侧,以A1P1为边长作正方形,与x轴交于A2.过A2作x轴的垂线与直线l交于点P2.在线段A2P2右侧,以A2P2长为边长作正方形,与x轴交于A3.按照此法做下去,则P3的坐标为