��Ŀ����
8���ھ���ABCD�У�AB=4��BC=8�������Խ��߽���O��ֱ��EF�Ƶ�O��ת���ֱ�AD��BC�ڵ�E��F������AF��CE����1����ͼ��1��������������������ͨ�ı��Ρ����Ρ���ͨƽ���ı��Ρ������λ���������ѡ����գ���ת�������ı���AFCEʼ��Ϊƽ���ı��Σ�
����EΪAD���е�ʱ�ı���AFCEΪƽ���ı��Σ�
��EF��ACʱ�ı���AFCEΪ���Σ�
��2����ͼ��1������EF��ACʱ����AF�ij���
��3����ͼ��2�����ڣ�2���Ļ����ϣ�������P��A���������A��F��B��A�˶�һ��ֹͣ���ٶ�Ϊÿ��5���ף�ͬʱ��Q��C���������C��D��E��C�˶�һ��ֹͣ���ٶ�Ϊÿ��4���ף���P��Q�˶������У��ڼ���ʱ���ı���APCQ��ƽ���ı��Σ�
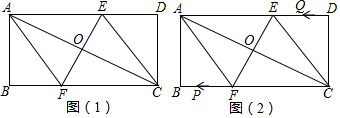
���� ��1����AAS֤����AOE�ա�COF���ó�AE=CF�����ɵó��ı���AFCEΪƽ���ı��Σ�����EΪAD���е�ʱ���ı���AFCEΪƽ���ı��Σ���EF��ACʱ���ó��ı���AFCEΪ���Σ�
��2�����ݹ��ɶ����ó����̣��ⷽ�̼�����AF�ij���
��3����������ۿ�֪��P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ�
��� �⣺��1������EΪAD���е�ʱ���ı���AFCEΪƽ���ı��Σ��������£�
���ı���ABCD�Ǿ��Σ�
��AD��BC��OA=OC��
���CAD=��ACB����AEF=��CFE��
�ڡ�AOE�͡�COF�У�$\left\{\begin{array}{l}{��CAD=��ACB}&{\;}\\{��AEF=��CFE}&{\;}\\{OA=OC}&{\;}\end{array}\right.$��
���AOE�ա�COF��AAS����
��AE=CF��
�֡�AE��CF��
���ı���AFCEΪƽ���ı��Σ�
����EΪAD���е�ʱ��AE=CF��AE��CF��
���ı���AFCEΪƽ���ı��Σ�
��EF��ACʱ���ı���AFCEΪ���Σ��������£�
���ɢ�֪�ı���AFCEΪƽ���ı��Σ�
��EF��AC��
���ı���AFCEΪ���Σ�
�ʴ�Ϊ��ƽ���ı��Σ�ƽ���ı��Σ����Σ�
��2���⣺�����εı߳�AF=CF=xcm����BF=��8-x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ����ã�AB2+BF2=AF2��
��42+��8-x��2=x2��
��ã�x=5��
��AF=5��
��3���⣺��������ã�P��AF��ʱ��Q��CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P��AB��ʱ��Q��DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
��ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��
PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12-4t��
��5t=12-4t��
��ã�t=$\frac{4}{3}$��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t=$\frac{4}{3}$�룮
���� �������ı����ۺ���Ŀ�������˾��ε����ʡ����ε��ж������ʡ����ɶ�����ƽ���ı��ε��ж������ʵ�֪ʶ�����ʱ������������ڲ�ͬ��λ�������ɵ�ͼ����״�ǽ����Ĺؼ���

| A�� | $\sqrt{0.1}$ | B�� | $\sqrt{\frac{1}{2017}}$ | C�� | $\sqrt{48}$ | D�� | $\sqrt{{a}^{2}+{b}^{2}}$ |
| A�� | 12 cm | B�� | 10 cm | C�� | 8 cm | D�� | 6 cm |
 ��ͼ��O�Ǿ���ABCD�Խ��ߵĽ��㣬AEƽ�֡�BAD����AOD=120�㣬���AEO=30�ȣ�
��ͼ��O�Ǿ���ABCD�Խ��ߵĽ��㣬AEƽ�֡�BAD����AOD=120�㣬���AEO=30�ȣ�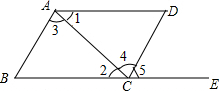 ��ͼ���������ж�AB��CD�������У���������
��ͼ���������ж�AB��CD�������У���������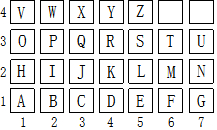 ij��Ӣ�ĵ��ʵ���ĸ˳���Ӧ����ͼ�е��������Էֱ�Ϊ��6��2������1��1������6��3������1��2������5��3������������Ӣ�ĵ���д����ΪMATHS��
ij��Ӣ�ĵ��ʵ���ĸ˳���Ӧ����ͼ�е��������Էֱ�Ϊ��6��2������1��1������6��3������1��2������5��3������������Ӣ�ĵ���д����ΪMATHS��