已知实数x满足x+$\frac{1}{x}+{x}^{2}+\frac{1}{{x}^{2}}$=0.求x+$\frac{1}{x}$的值．题目和参考答案——青夏教育精英家教网—

题目内容

18．已知实数x满足x+$\frac{1}{x}+{x}^{2}+\frac{1}{{x}^{2}}$=0，求x+$\frac{1}{x}$的值．

分析已知方程变形后，设x+$\frac{1}{x}$=y，求出方程的解得到y的值，即可确定出所求式子的值．

解答解：设x+$\frac{1}{x}$=y，方程变形得：（x+$\frac{1}{x}$）²+（x+$\frac{1}{x}$）-2=0，即y²+y-2=0，
整理得：（y+2）（y-1）=0，
解得y=-2或y=1．
所以x+$\frac{1}{x}$=-2或x+$\frac{1}{x}$=1．

点评此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

练习册系列答案

9．抛物线上有三点（1，3）、（3，3）、（2，1），此抛物线的解析式为y=2x²-8x+9．

-$\frac{3}{4}$＜-$\frac{4}{5}$

C．

|-5|＜|-5$\frac{1}{2}$|

D．

1.7＞-1.7

13．已知关于x的方程x²-kx+1=0有两个相等的实数根．求k的值．

3．

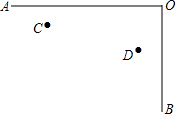城北中学八（2）班举行文艺晚会，桌子摆成两直条（如图中的AO，BO），AO桌面上摆满了桔子，OB桌面上摆满了糖果，站在C处的学生小明先到AO桌面上拿桔子，再到OB桌面上拿糖果，然后回到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短．

10．若m是从0，1，2，三个数中任取的一个数，n是从0，2两个数中任取的一个数，那么关于x的一元二次方程x²-2mx+n=0有实数根的概率为$\frac{2}{3}$．

7．用不同的分组分解法将下列多项式分解因式：
（1）ax+ay+bx+by；
（2）a²-b²-c²+2bc；
（3）a²-2ab+b²+2a-2b+1．

8．

如图，△ABC是一个等腰三角形钢架，现要在横梁BC上确定一点D，使△ABD≌△ACD，点D的位置应当选在何处？为什么？

试题分类