题目内容
8.△ABC的3条边的长分别为6、8、10,与其相似的△DEF的最长边为15,则△DEF的最短边为4,△DEF的面积为54.分析 设△DEF的最短边为x,再由相似三角形的性质即可得出结论.
解答 解:设△DEF的最短边为x,
∵△ABC的3条边的长分别为6、8、10,与其相似的△DEF的最长边为15,
∴$\frac{x}{6}$=$\frac{10}{15}$,解得x=4.
∵62+82=102,
∴△ABC是直角三角形,
∴S△ABC=$\frac{1}{2}$×6×8=24.
∵$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=($\frac{4}{6}$)2=$\frac{24}{{S}_{△DEF}}$,解得△DEF的面积=54.
故答案为:4,54.
点评 本题考查的是相似三角形的性质,熟知相似三角形的面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某校组织学生开展植树活动.为了解全校学生的植树情况,学校随机抽查了20名学生的植树数量,并将调查数据整理如表:
请根据表格提供的信息回答下列问题:
(1)调查的植树数量的众数是2棵;
(2)求这20名学生的植树数量的平均数;
(3)若该校共有500名学生,请根据调查的数据估计该校学生的植树总数约是多少棵?
| 植树数量(单位:棵) | 1 | 2 | 3 | 4 | 5 |
| 人数(单位:人) | 4 | 8 | 4 | 2 | 2 |
(1)调查的植树数量的众数是2棵;
(2)求这20名学生的植树数量的平均数;
(3)若该校共有500名学生,请根据调查的数据估计该校学生的植树总数约是多少棵?
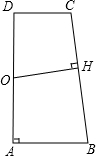 如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=4,CD=3,BC=7,O为AD边的中点,则点O到BC的距离为2$\sqrt{3}$.
如图,在梯形ABCD中,AB∥DC,∠A=90°,AB=4,CD=3,BC=7,O为AD边的中点,则点O到BC的距离为2$\sqrt{3}$.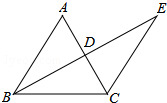 如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=64°,则∠E=32°.
如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=64°,则∠E=32°.