题目内容
如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
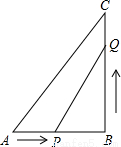
(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5cm?
(3)如果P、Q分别从A、B同时出发,△PBQ的面积能否等于8cm2?说明理由.由此思考:△PBQ的面积最多为多少cm2?
见解析
【解析】
试题分析:(1)设运动t秒后△PBQ的面积等于4,用t表示出BP、BQ的长,利用三角形面积公式可得方程解方程即可;(2)在△PBQ中,根据勾股定理,得PQ2=BP2+BQ2,把BP、BQ代入可得方程,解方程即可;(3)根据三角形的面积公式,得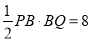 , t(5-t)=8, t2-5t+8=0,然后判断方程根的情况,方程无根说明△PBQ的面积不能等于8cm2.
, t(5-t)=8, t2-5t+8=0,然后判断方程根的情况,方程无根说明△PBQ的面积不能等于8cm2.
试题解析:设运动t秒后△PBQ的面积等于4,根据题意,知BP=AB-AP=5-t,BQ=2t.
(1)根据三角形的面积公式,得
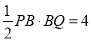 ,t(5-t)=4, t2-5t+4=0, 解得t=1或4秒.
,t(5-t)=4, t2-5t+4=0, 解得t=1或4秒.
故1或4秒后,△PBQ的面积等于4cm2.
(2)根据勾股定理,得
PQ2=BP2+BQ2=(5-t)2+(2t)2=25,
5t2-10t=0, ∵t≠0, ∴t=2.
故2秒后,PQ的长度等于5cm.
(3)根据三角形的面积公式,得
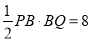 , t(5-t)=8, t2-5t+8=0,
, t(5-t)=8, t2-5t+8=0,
△=(-5)2-4×1×8=-7<0.
故△PBQ的面积不能等于8cm2.
∵t(5-t)=-(t-2.5)2+6.25,∴△PBQ的面积最多为6.25cm2.
考点:1.勾股定理;2.一元二次方程;3.配方法.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案



 是方程
是方程 的两个实数根,则
的两个实数根,则 _______
_______

 ·(
·( )n B.
)n B.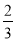
 ·(
·(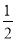 )n
)n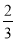 ·(
·( )n-1 D.
)n-1 D.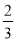
 ·(
·( )n-
)n-