��Ŀ����
 ������ѧϰ��
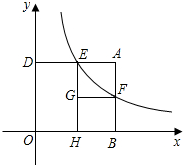
������ѧϰ����ͼ������ABOD������OB��OD������������������ϣ�OD=3���������뷴��������y=
| k |
| x |
�ٸ÷����������Ľ���ʽ��ʲô��
�ڵ��ı���AEGFΪ������ʱ����F�������Ƕ��٣�
��1���Ķ�����ѧϰ���ݣ��������е����⣻
��2��С����һ���о��ı���AEGF��������������⣺����AE��EGʱ������AEGF�����DOHE�ܷ�ȫ�ȣ��ܷ����ƣ���
���С����������⣬�����ж������������ܷ�ȫ�ȣ�ֱ��д�����ۼ��ɣ������������ܷ����ƣ��������ƣ�������Ʊȣ����������ƣ���˵�����ɣ�
���㣺�����������ۺ���
ר�⣺�ۺ���
��������1�����ȸ��ݾ��ε����ʵõ�D��2��3����Ȼ�����÷���������ͼ���ϵ���������������k=6����õ���������������ʽΪy=
��
����������AEGF�ı߳�Ϊa����AE=AF=a������������ͼ�εĹ�ϵ�õ�B��2+a��0������A��2+a��3��������F������Ϊ��2+a��3-a�����������÷���������ͼ���ϵ�����������ã�2+a����3-a��=6��Ȼ���һԪ���η��̿�ȷ��a��ֵ���Ӷ��õ�F�����ꣻ
��2����AE��EGʱ���������AEGF�����DOHEȫ�ȣ���AE=OD=3��AF=DE=2����õ�F������Ϊ��3��3�������ݷ���������ͼ���ϵ�������������жϵ�F��3��3�����ڷ���������y=
��ͼ���ϣ��ɴ˵õ�����AEGF�����DOHE����ȫ�ȣ�
��AE��EGʱ��������AEGF�����DOHE���ƣ��������Ƶ����ʵ�AE��OD=AF��DE����
=
=
����AE=3t����AF=2t���õ�F������Ϊ��2+3t��3-2t����
���÷���������ͼ���ϵ�����������ã�2+3t����3-2t��=6�����t1=0����ȥ����t2=
����AE=3t=
�����ǵõ����Ʊ�=
=
��
| 6 |
| x |
����������AEGF�ı߳�Ϊa����AE=AF=a������������ͼ�εĹ�ϵ�õ�B��2+a��0������A��2+a��3��������F������Ϊ��2+a��3-a�����������÷���������ͼ���ϵ�����������ã�2+a����3-a��=6��Ȼ���һԪ���η��̿�ȷ��a��ֵ���Ӷ��õ�F�����ꣻ
��2����AE��EGʱ���������AEGF�����DOHEȫ�ȣ���AE=OD=3��AF=DE=2����õ�F������Ϊ��3��3�������ݷ���������ͼ���ϵ�������������жϵ�F��3��3�����ڷ���������y=
| 6 |
| x |
��AE��EGʱ��������AEGF�����DOHE���ƣ��������Ƶ����ʵ�AE��OD=AF��DE����
| AE |
| AF |
| OD |
| DE |
| 3 |
| 2 |
���÷���������ͼ���ϵ�����������ã�2+3t����3-2t��=6�����t1=0����ȥ����t2=
| 5 |
| 6 |
| 5 |
| 2 |
| AE |
| OD |
| 5 |
| 6 |
��� �⣺��1���١��ı���ABODΪ���Σ�EH��x�ᣬ
�⣺��1���١��ı���ABODΪ���Σ�EH��x�ᣬ
��OD=3��DE=2��
��E��������2��3����
��k=2��3=6��
�෴������������ʽΪy=
��x��0����
����������AEGF�ı߳�Ϊa����AE=AF=a��
��B��������2+a��0������A��������2+a��3����
��F��������2+a��3-a����
��F��2+a��3-a������y=
�ã�2+a����3-a��=6�����a1=1��a2=0����ȥ����
��F��������3��2����
��2���ٵ�AE��EGʱ������AEGF�����DOHE����ȫ�ȣ��������£�
�������AEGF�����DOHEȫ�ȣ���AE=OD=3��AF=DE=2��
��A��������5��3����
��F��������3��3����
��3��3=9��6��
��F�㲻�ڷ���������y=
��ͼ���ϣ�
�����AEGF�����DOHE����ȫ�ȣ�
�ڵ�AE��EGʱ������AEGF�����DOHE�����ƣ�
�߾���AEGF�����DOHE�����ƣ�
��AE��OD=AF��DE��
��
=
=
��
��AE=3t����AF=2t��
��A��������2+3t��3����
��F��������2+3t��3-2t����
��F��2+3t��3-2t������y=
�ã�2+3t����3-2t��=6�����t1=0����ȥ����t2=
��
��AE=3t=
��
�����Ʊ�=
=
=
��
 �⣺��1���١��ı���ABODΪ���Σ�EH��x�ᣬ
�⣺��1���١��ı���ABODΪ���Σ�EH��x�ᣬ��OD=3��DE=2��
��E��������2��3����
��k=2��3=6��
�෴������������ʽΪy=
| 6 |
| x |
����������AEGF�ı߳�Ϊa����AE=AF=a��
��B��������2+a��0������A��������2+a��3����
��F��������2+a��3-a����
��F��2+a��3-a������y=
| 6 |
| x |
��F��������3��2����
��2���ٵ�AE��EGʱ������AEGF�����DOHE����ȫ�ȣ��������£�
�������AEGF�����DOHEȫ�ȣ���AE=OD=3��AF=DE=2��
��A��������5��3����
��F��������3��3����
��3��3=9��6��
��F�㲻�ڷ���������y=
| 6 |
| x |
�����AEGF�����DOHE����ȫ�ȣ�
�ڵ�AE��EGʱ������AEGF�����DOHE�����ƣ�
�߾���AEGF�����DOHE�����ƣ�
��AE��OD=AF��DE��
��
| AE |
| AF |
| OD |
| DE |
| 3 |
| 2 |
��AE=3t����AF=2t��
��A��������2+3t��3����
��F��������2+3t��3-2t����
��F��2+3t��3-2t������y=
| 6 |
| x |
| 5 |
| 6 |
��AE=3t=
| 5 |
| 2 |
�����Ʊ�=
| AE |
| OD |
| ||
| 3 |
| 5 |
| 6 |
���������⿼���˷������������ۺ��⣺���շ���������ͼ���ϵ���������������ε����ʺ�ͼ��ȫ�ȵ����ʡ����Ƶ����ʣ�����ͼ��������Ĺ�ϵ�����һԪ���η��̣�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

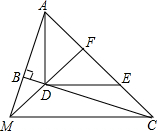 ��ͼ����ABC=90�㣬D��E�ֱ���BC��AC�ϣ�AD��DE����AD=DE����F��AE���е㣬FD��AB�ཻ�ڵ�M��
��ͼ����ABC=90�㣬D��E�ֱ���BC��AC�ϣ�AD��DE����AD=DE����F��AE���е㣬FD��AB�ཻ�ڵ�M��
 Ϊ��ά������Ȩ�棬���齨�Ĺ��Һ���ּ�ǿ�˺���Ѳ�����ȣ���ͼ��һ�Һ��ബλ�ڵ���P��ƫ��45�㷽�������100�����A����������������һ��ʱ�����λ�ڵ���P��ƫ��30�㷽���ϵ�B����
Ϊ��ά������Ȩ�棬���齨�Ĺ��Һ���ּ�ǿ�˺���Ѳ�����ȣ���ͼ��һ�Һ��ബλ�ڵ���P��ƫ��45�㷽�������100�����A����������������һ��ʱ�����λ�ڵ���P��ƫ��30�㷽���ϵ�B����
 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3������B��-2��1������x���ϴ��ڵ�P��A��B����ľ���֮����С����P���������
��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3������B��-2��1������x���ϴ��ڵ�P��A��B����ľ���֮����С����P���������