题目内容
 如图,在平面直角坐标系中,已知点A(2,3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是
如图,在平面直角坐标系中,已知点A(2,3),点B(-2,1),在x轴上存在点P到A,B两点的距离之和最小,则P点的坐标是考点:轴对称-最短路线问题,坐标与图形性质
专题:压轴题
分析:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,求出C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出k、b,得出直线BC的解析式,求出直线与x轴的交点坐标即可.
解答: 解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
∵A点的坐标为(2,3),B点的坐标为(-2,1),
∴C(2,-3),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:
解得
.
即直线BC的解析式是y=-x-1,
当y=0时,-x-1=0,
解得:x=-1,
∴P点的坐标是(-1,0).
故答案为:(-1,0).
 解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,
解:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,∵A点的坐标为(2,3),B点的坐标为(-2,1),
∴C(2,-3),
设直线BC的解析式是:y=kx+b,
把B、C的坐标代入得:
|
解得
|
即直线BC的解析式是y=-x-1,
当y=0时,-x-1=0,
解得:x=-1,
∴P点的坐标是(-1,0).
故答案为:(-1,0).
点评:本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,关键是能找出P点,题目具有一定的代表性,难度适中.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 【合作学习】
【合作学习】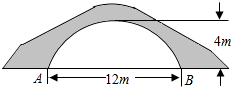 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=- 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(6,
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(6, 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.