题目内容
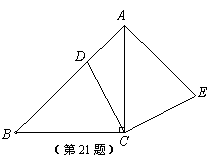
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
 |
(1)解:∵∠ACB=90°∴∠BCD+∠ACD=90°∵∠DCE=90°∴∠ACD+∠ACE=90°
∴∠BCD=∠ACE………………………………………………………………………1分
在△CBD与△CAE中,∵CB=CA, ∠BCD=∠ACE,CD=CE,∴△CBD≌△CAE,
∴∠B=∠CAE, ………………………………………………………………………3分
∵∠B+∠BAC=90°∴∠BAC+∠EAC=90°∴AB⊥AE …………………………4分
(2)证:∵点D为AB中点,∴∠ADC=90°………………………………………6分
∵∠DCE=90°, ∠BAE=90°∴四边形ADCE是矩形,…………………………7分
∴CD=CE,∴四边形ADCE是正方形 ……………………………………………8分

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
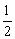 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为x,另有一个被均匀分成4份的转盘,上面分别标有数字-1、0、-4、-5,转动转盘,指针所指的数字记为y(若指针指在分割线上则重新转一次),请你用画树状图或列表格的方法求出点P(x,y)落在抛物线y=2x2-2x-4与x轴所围成的区域内(不含边界)的概率.
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为x,另有一个被均匀分成4份的转盘,上面分别标有数字-1、0、-4、-5,转动转盘,指针所指的数字记为y(若指针指在分割线上则重新转一次),请你用画树状图或列表格的方法求出点P(x,y)落在抛物线y=2x2-2x-4与x轴所围成的区域内(不含边界)的概率. 中自变量x的取值范围是 .
中自变量x的取值范围是 .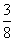 x2-
x2-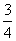 x+3与x轴交于
x+3与x轴交于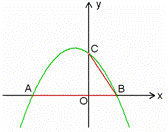
 ,则点
,则点 轴对称的点的坐标是
轴对称的点的坐标是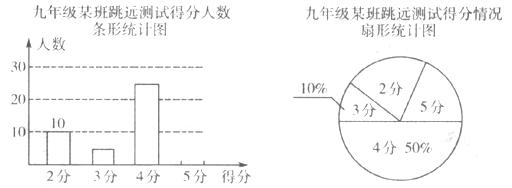
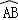 的长为( )
的长为( )