题目内容
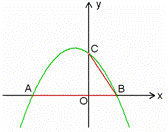
如图1,抛物线y=-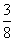 x2-
x2-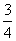 x+3与x轴交于
x+3与x轴交于
A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等
于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4, 0),M为直线l上的动点,当以A、B、M为
顶点所作的直角三角形有且只有三个时,求直线l的解析式.
|
|
|
 |
解(1)由-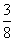 x2-
x2-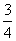 x+3=0, 得交点坐标为A(-4, 0)、B(2, 0)
x+3=0, 得交点坐标为A(-4, 0)、B(2, 0)
(2)△ACD与△ACB有公共的底边AC,当△ACD的面积等于△ACB的面积时,点B、D到直线AC的距离相等.
过点B作AC的平行线交抛物线的对称轴于点D,在AC的另一侧有对应的点D′.
设抛物线的对称轴与x轴的交点为G,与AC交于点H.
由BD//AC,得∠DBG=∠CAO.所以 . ………………………………4分
. ………………………………4分
所以 ,点D的坐标为
,点D的坐标为 .…………………………………………5分
.…………………………………………5分
因为AC//BD,AG=BG,所以HG=DG.
而D′H=DH,所以D′G=3DG .所以D′的坐标为
.所以D′的坐标为 …………6分
…………6分

图2 图3
(3)过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点M.
以AB为直径的⊙G如果与直线l相交,那么就有2个点M;如果圆与直线l相切,就只有1个点M了. …………………………………………………………………………………7分
连接GM,那么GM⊥l.
在Rt△EGM中,GM=3,GE=5,所以EM=4.
在Rt△EM1A中,AE=8, ,所以M1A=6.…………………8分
,所以M1A=6.…………………8分
所以点M1的坐标为(-4, 6),过M1、E的直线l为y=-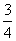 x+3. …………9分
x+3. …………9分
根据对称性,直线l还可以是y=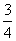 x-3. …………10分
x-3. …………10分

 名校课堂系列答案
名校课堂系列答案
 是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; x2-
x2- x-
x- 是闭区间[a,b]上的“闭函数”,求实数a、b的值.
是闭区间[a,b]上的“闭函数”,求实数a、b的值. ,(x1,y1),(x2,y2)为函数图象
,(x1,y1),(x2,y2)为函数图象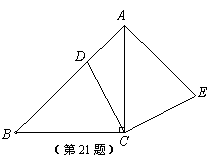
 103吨 B.67.5×103吨 C.6.75
103吨 B.67.5×103吨 C.6.75  的根可看作是函数
的根可看作是函数 的图像与函数
的图像与函数 的图像交点的横坐标。类似地,利用这种图像法,可以确定方程
的图像交点的横坐标。类似地,利用这种图像法,可以确定方程 的实数根
的实数根 所在的范围是
所在的范围是
 B.
B. C.
C. D.
D.
 B.-2 C.0 D.1
B.-2 C.0 D.1 )是关于x的方程
)是关于x的方程 的根,则m+n的值为 .
的根,则m+n的值为 .