题目内容
16. 如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.
如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出△CAD是直角三角形,分别求出△ABC和△CAD的面积,即可得出答案.
解答 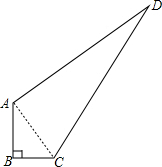 解:连结AC,
解:连结AC,
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5(m),
S△ABC=$\frac{1}{2}$×3×4=6(m2),
在△ACD中,
∵AD=12m,AC=5m,CD=13m,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD=$\frac{1}{2}$×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
点评 本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出△ABC和△CAD的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
2015年5月份,该市居民甲用电100千瓦时,交费60元;居民乙用电200千瓦时,交费122.5元.
(1)求上表中a、b的值.
(2)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月交费277.5元?
(3)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价等于0.62元/千瓦时?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的部分 | a |
| 超过150千瓦时,但不超过300千瓦时的部分 | b |
| 超过300千瓦时的部分 | a+0.3 |
(1)求上表中a、b的值.
(2)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月交费277.5元?
(3)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价等于0.62元/千瓦时?
1.已知a<0,b<0,且|a|<|b|,则|a+b|-|b-a|+|a-b|的化简结果为( )
| A. | -a-b | B. | 2a+b | C. | a-b | D. | -a-2b |
8.下列表情中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 在平面直角坐标系中,O是原点,已知点A(1,3)、B(4,1).直线l是一次函数y=x+b的图象.
在平面直角坐标系中,O是原点,已知点A(1,3)、B(4,1).直线l是一次函数y=x+b的图象.