题目内容
1．
如图，已知直线AB和CD相交于点O，OE⊥AB，∠AOD=128°，则∠COE的度数是（ ）| A． | 52° | B． | 48° | C． | 42° | D． | 38° |
分析 首先由邻补角的定义可求得∠AOC的度数，然后由垂线的定义可求得∠AOE=90°，从而可求得∠COE的度数．
解答 解：∵∠AOD+∠AOC=180°，
∴∠AOC=180°-128°=52°．
∵OE⊥AB，
∴∠AOE=90°．
∴∠COE=∠AOE-∠AOC=90°-52°=38°．
故选：D．
点评 本题主要考查的是邻补角的性质、垂线的定义，求邻边角的性质求得∠AOC=52°是解题的关键．
练习册系列答案
相关题目
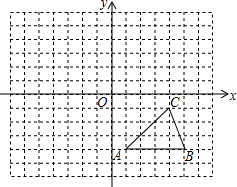如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，
6．下列各数中，最大的数是（ ）
| A． | |-2| | B． | $\sqrt{2}$ | C． | -（-1.5） | D． | 20 |
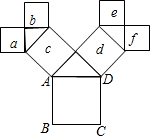如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形ABCD的边长为6，则正方形a，b，c，d，e，f的面积和为72．