题目内容
13. 如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为61°.
如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为61°.
分析 首先连接OD,由直角三角板ABC的斜边AB与量角器的直径恰好重合,可得点A,B,C,D共圆,又由点D对应的刻度是58°,利用圆周角定理求解即可求得∠BCD的度数,继而求得答案.
解答  解:连接OD,
解:连接OD,
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,
∴点A,B,C,D共圆,
∵点D对应的刻度是58°,
∴∠BOD=58°,
∴∠BCD=$\frac{1}{2}$∠BOD=29°,
∴∠ACD=90°-∠BCD=61°.
故答案为:61°.
点评 此题考查了圆周角定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.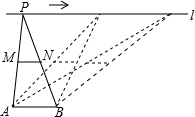 如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
 如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
| A. | ②③ | B. | ②⑤ | C. | ①③④ | D. | ④⑤ |
4. 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )
 如图,AB∥CD,∠A=50°,则∠1的大小是( )
如图,AB∥CD,∠A=50°,则∠1的大小是( )| A. | 50° | B. | 120° | C. | 130° | D. | 150° |
1.漳州市被国家交通运输部列为国家公路运输枢纽城市,现拥有营运客货车月21000辆,21000用科学记数法表示为( )
| A. | 0.21×104 | B. | 21×103 | C. | 2.1×104 | D. | 2.1×103 |
2.下列运算正确的是( )
| A. | a6÷a3=a2 | B. | 5a2-3a2=2a | C. | (a3)3=a9 | D. | (a-b)2=a2-b2 |
3. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 正方体 |