题目内容
3.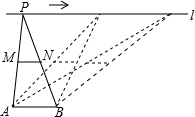 如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )
| A. | ②③ | B. | ②⑤ | C. | ①③④ | D. | ④⑤ |
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=$\frac{1}{2}$AB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
解答 解:∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MN=$\frac{1}{2}$AB,
即线段MN的长度不变,故①错误;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②正确;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③错误;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小点P的移动而变化,故⑤正确.
综上所述,会随点P的移动而变化的是②⑤.
故选:B.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等底等高的三角形的面积相等,平行线间的距离的定义,熟记定理是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18. 在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
 在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )| A. | 段① | B. | 段② | C. | 段③ | D. | 段④ |
8.下面四个几何体中,俯视图为四边形的是( )
| A. |  | B. |  | C. |  | D. |  |
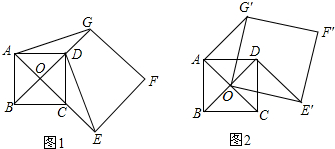
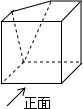 如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )

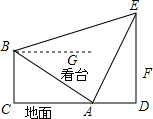 如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)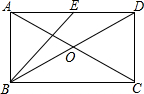 如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)
如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$) 如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为61°.
如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为61°.