题目内容
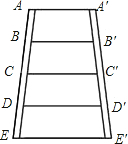 如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60cm,EE′=80cm.则BB′的长为( )
如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60cm,EE′=80cm.则BB′的长为( )| A、0.65m |
| B、0.675m |
| C、0.725m |
| D、0.75m |
考点:相似三角形的应用
专题:
分析:过点A作AE″∥A′E′与BB′相交于点B″,与EE′相交于E″,可得四边形AE″E′A′是平行四边形,根据平行四边形的对边相等可得E′E″=AA′,然后求出EE″,再根据△ABB″和△AEE″相似,利用相似三角形对应边成比例列式求出BB″,然后根据BB′=BB″+B″B′计算即可得解.
解答: 解:如图,过点A作AE″∥A′E′与BB′相交于点B″,与EE′相交于E″,
解:如图,过点A作AE″∥A′E′与BB′相交于点B″,与EE′相交于E″,
∵AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,
∴AA′∥BB′∥CC′∥DD′∥EE′,
∴四边形AE″E′A′是平行四边形,
∴E′E″=AA′=60cm,
∴EE″=80-60=20cm,
∵BB′∥EE′,
∴△ABB″∽△AEE″,
∴
=
=
,
∴BB″=20×
=5cm,
∴BB′=BB″+B″B′=5+60=65cm=0.65m.
故选A.
 解:如图,过点A作AE″∥A′E′与BB′相交于点B″,与EE′相交于E″,
解:如图,过点A作AE″∥A′E′与BB′相交于点B″,与EE′相交于E″,∵AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,
∴AA′∥BB′∥CC′∥DD′∥EE′,
∴四边形AE″E′A′是平行四边形,
∴E′E″=AA′=60cm,
∴EE″=80-60=20cm,
∵BB′∥EE′,
∴△ABB″∽△AEE″,
∴
| BB″ |
| EE″ |
| AB |
| AE |
| 1 |
| 4 |
∴BB″=20×
| 1 |
| 4 |
∴BB′=BB″+B″B′=5+60=65cm=0.65m.
故选A.
点评:本题考查了相似三角形的应用,平行四边形的判定与性质,作辅助线构造出平行四边形和相似三角形是解题的关键.

练习册系列答案
相关题目
“五•一”以来,随着枇杷的大量上市,某超市的枇杷每千克降价a元后,再打八折促销,现售价为b元/千克,则原来的价格为( )
A、(a-
| ||
B、(a+
| ||
| C、(a+5b)元/千克 | ||
| D、(a-5b)元/千克 |
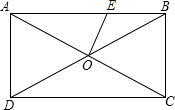 如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD=
如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD=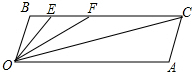 如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.