题目内容
7. 已知直线y1=$\frac{3}{2}$x+$\frac{3}{2}$及直线y2=-x+4.
已知直线y1=$\frac{3}{2}$x+$\frac{3}{2}$及直线y2=-x+4.(1)直线y2=-x+4与y轴的交点坐标为(0,4);
(2)在所给的平面直角坐标系(如图)中画出这两条直线的图象;
(3)求这两条直线以及x轴所围成的三角形面积.
分析 (1)在y2=-x+4中令x=0,可求得与y轴的交点坐标;
(2)由两直线的解析式可画出函数图象;
(3)可先求得直线y1与x轴的交点,结合(1)可求得三角形的底,再求两直线的交点,由交点坐标可求得该三角形的高,可求得三角形的面积.
解答 解:(1)在y2=-x+4中,令x=0,可得y2=4,
∴直线y2=-x+4与y轴的交点坐标为(0,4),
故答案为:(0,4);
(2)在y1=$\frac{3}{2}$x+$\frac{3}{2}$中,令x=0,可得y1=$\frac{3}{2}$,令y1=0,可得x=-1,
∴直线y1与y轴交于点A(0,$\frac{3}{2}$),与x轴交于点B(-1,0);
在y2=-x+4中,令y2=0,可求得x=4,
∴直线y2与x轴交于点C(4,0),且由(1)可知与y轴交于点D(0,4),联立两直线解析式可得$\left\{\begin{array}{l}{y=\frac{3}{2}x+\frac{3}{2}}\\{y=-x+4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,
∴两直线的交点E(1,3),
∴两直线的图象如图所示;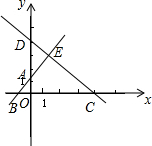
(3)由(2)可知BC=4-(-1)=5,
且E到BC的距离为3,
∴S△BCE=$\frac{1}{2}$×5×3=7.5.
点评 本题主要考查一次函数的交点,掌握两函数交点坐标的求法是解题的关键,即联立两函数解析式求方程组的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若$\sqrt{x-1}$的在实数范围内有意义,则( )
| A. | x≥1 | B. | x≠1 | C. | x>1 | D. | x≤1 |
12.直角三角形的两条直角边长为3和4,则该直角三角形斜边上的高为( )
| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | $\frac{24}{5}$ |
16.下列图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 菱形 | B. | 平行四边形 | C. | 等边三角形 | D. | 梯形 |
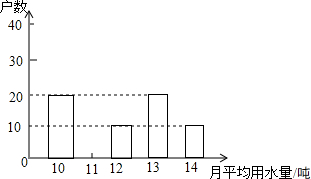 市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.