题目内容
19．
如图，正方形ABCD内接于⊙O，点P在弧$\widehat{AB}$上，则∠DPC=45°．
分析 连接OD、OC，根据正方形的性质，易得出∠DOC=90°，根据圆周角定理，可求出∠DPC=45°．
解答 解：连接OD、OC，则∠P=$\frac{1}{2}$∠DOC，
∵O是正方形外接圆的圆心，
∴∠DOC=90°，
∴∠DPC=$\frac{1}{2}$∠DOC=45°．
故答案为：45°
点评 此题考查圆心角与圆周角的问题，正确理解圆心角与圆周角的关系是解决本题的关键．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
PQ B. AQ＝3PQ C. AQ＝
PQ D. AQ＝4PQ
10．
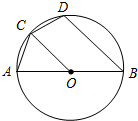如图，AB为⊙O的直径，弦AC=CD．
（1）连结BD，OC，则OC，DB的位置关系是OC∥BD；
（2）若AC=CD=1，BD=4，则半径OC的长等于$\frac{2+\sqrt{6}}{2}$．
如图，AB为⊙O的直径，弦AC=CD．（1）连结BD，OC，则OC，DB的位置关系是OC∥BD；
（2）若AC=CD=1，BD=4，则半径OC的长等于$\frac{2+\sqrt{6}}{2}$．
如图，在Rt△ABC中，∠B=90°，AC=10cm，BC=6cm，现有两点P、Q的分别从点A和点C同时出发，沿边AB，CB向终点B移动．已知点P，Q的速度分别为2cm/s，1cm/s，且当其中一点到达终点时，另一点也随之停止移动，设P，Q两点移动时间为xs．问是否存在这样的x，使得四边形APQC的面积等于16cm2？若存在，请求出此时x的值；若不存在，请说明理由．
如图，已知$\widehat{CE}$的度数为80°，$\widehat{BD}$的度数为30°，则∠A=50°．
11．
为了庆祝2016年的G20峰会在杭州举办，七年级同学在班会课进行了趣味活动．小舟同学在模板上画出一个菱形ABCD，将它以点O为中心按顺时针方向分别旋转90°、180°、270°后得到如图所示的图形，其中∠ABC=120°，AB=10cm．然后小舟将此图形制作成一个靶子，那么当我们投飞镖时命中阴影部分的概率为（ ）
为了庆祝2016年的G20峰会在杭州举办，七年级同学在班会课进行了趣味活动．小舟同学在模板上画出一个菱形ABCD，将它以点O为中心按顺时针方向分别旋转90°、180°、270°后得到如图所示的图形，其中∠ABC=120°，AB=10cm．然后小舟将此图形制作成一个靶子，那么当我们投飞镖时命中阴影部分的概率为（ ）| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $2-\sqrt{3}$ | C． | $\sqrt{3}-1$ | D． | $\frac{1}{2}$ |
在矩形ABCD中，AB=12cm，BC=6cm，点P从点A出发沿AB以2cm/s的速度向点B移动；同时，点Q从点B出发沿BC以1cm/s的速度向点C移动，点P运动到点B时，点Q也停止运动，几秒钟后△PQC的面积等于16cm2？