题目内容
【题目】甲、乙两人先后从公园大门出发，沿绿道向码头步行，乙先到码头并在原地等甲到达．图1是他们行走的路程y（m）与甲出发的时间x（min）之间的函数图象．
（1）求线段AC对应的函数表达式；
（2）写出点B的坐标和它的实际意义；
（3）设d（m）表示甲、乙之间的距离，在图2中画出d与x之间的函数图象（标注必要数据）．
【答案】（1）y=100x﹣600；（2）点B的坐标为（15，900），它的实际意义是当甲出发15分钟后被乙追上，此时他们距出发点900米；（3）d=60x；d=﹣40x+600；d=40x﹣600；d=1500﹣60x．
【解析】
（1）根据图1中的数据可以得出线段AC对应的函数表达式；
（2）设直线OD的解析式为y=mx，将D（25，1500）代入，求出m的值，再联立一次函数y=100x﹣600，即可求出B的坐标；
（3）分情况讨论x的求值范围并求出相对应的函数关系式.
解：（1）设线段AC对应的函数表达式为y=kx+b（k≠0）．
将A（6，0）、C（21，1500）代入，
得
，解得
，
所以线段AC对应的函数表达式为y=100x﹣600；
（2）设直线OD的解析式为y=mx，
将D（25，1500）代入，
得25m=1500，解得m=60，
∴直线OD的解析式为y=60x．
由
，解得
，
∴点B的坐标为（15，900），它的实际意义是当甲出发15分钟后被乙追上，此时他们距出发点900米；
（3）①当0≤x≤6时，d=60x；
②当6＜x≤15时，d=60x﹣（100x﹣600）=﹣40x+600；
③当15＜x≤21时，d=100x﹣600﹣60x=40x﹣600；
④当21＜x≤25时，d=1500﹣60x．
d与x之间的函数图象如图所示：
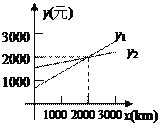
【题目】航拍无人机甲从海拔
处出发，以
匀速铅直上升，与此同时，航拍无人机乙从海拔
处出发，以
匀速铅直上升．设无人机上升时间为
，无人机甲、乙所在位置的高度分别为
、
（1）根据题意，填写下表：
上升时间 | 5 | 10 |
|
| 25 |
| |
| 60 |
|
（2）请你分别写出、
与
的关系式；
（3）在某时刻两架无人机能否位于同一高度？若能，求无人机上升的时间和所在高度；若不能，请说明理由．
【题目】随着地铁和共享单车的发展，“地铁
单车”已成为很多市民出行的选择，李华从学院路站出发，先乘坐地铁，准备在离家较近的
， 
， 
， 
， 
中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与学院路距离为
（单位：千米），乘坐地铁的时间
(单位：分钟)是关于
的一次函数，其关系如下表：
地铁站 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（
）求
关于
的函数表达式．
（
）李华骑单车的时间
(单位：分钟)与
的关系式为
，求李华从学院路站回到家的最短总时间，并指出他在哪一站出地铁．
