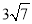题目内容
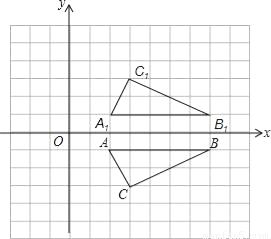
如图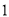 ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
( )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
( )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
( )如图2,在(
)如图2,在( )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+ AE'的最小值.
AE'的最小值.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
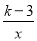 图象在二、四象限,则k的取值范围是( )
图象在二、四象限,则k的取值范围是( )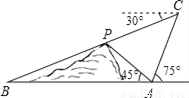
 )甲3局全胜的概率是__________;
)甲3局全胜的概率是__________; )如果甲队已经赢得了第1局比赛,那么甲队最终获胜的概率是多少?(用“树状图”或“列表”法写出解答过程)
)如果甲队已经赢得了第1局比赛,那么甲队最终获胜的概率是多少?(用“树状图”或“列表”法写出解答过程)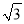 ),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )
),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )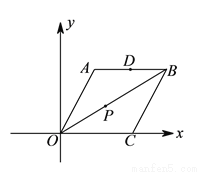
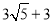 B.
B. 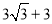 C.
C. 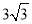 D.
D.