题目内容
 直线y=
直线y=| 1 | 2 |
(1)求点P的坐标;
(2)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当BR∥AP时,求点R的坐标.
分析:(1)因为P是直线与反比例函数在第一象限内的一个交点,设P(a,
a+2),用a表示AB,PB,根据S△ABP=9可以求出a,从而求出P的坐标;
(2)根据P的坐标可以求出反比例函数的解析式,设R(b,
),利用BR∥AP可以得到△AOC∽△BTR,再利用相似三角形的性质-对应边成比例可以得到关于b的方程,解方程求出b,也就求出了R的坐标.
| 1 |
| 2 |
(2)根据P的坐标可以求出反比例函数的解析式,设R(b,
| 6 |
| b |
解答: 解:(1)∵直线y=
解:(1)∵直线y=
x+2分别交x轴、y轴于A、C
∴A(-4,0)C(0,2).
设P(a,
a+2).即:AB=4+a,PB=
a+2
∴S△ABP=
×(a+4)(
a+2)=9
∴a=2或a=-10(舍)
∴a=2
即P(2,3).
(2)∵设反比例函数解析式为:y=
(k≠0),
∵P(2,3),
∴k=6,
∴反比例函数解析式为:y=
,
∵BR∥AP,
∴△AOC∽△BTR,
∴
=
,
设R(b,
),即:BT=b-2,RT=
,
∴
=
,
∴b2-2b-12=0,
∴b=1+
或b=1-
(舍),
∴R(1+
,
).
即R的坐标为(1+
,
).
 解:(1)∵直线y=
解:(1)∵直线y=| 1 |
| 2 |
∴A(-4,0)C(0,2).
设P(a,
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
∴a=2或a=-10(舍)
∴a=2
即P(2,3).
(2)∵设反比例函数解析式为:y=
| k |
| x |
∵P(2,3),

∴k=6,
∴反比例函数解析式为:y=
| 6 |
| x |
∵BR∥AP,
∴△AOC∽△BTR,
∴
| AO |
| BT |
| CO |
| RT |
设R(b,
| 6 |
| b |
| 6 |
| b |
∴
| 4 |
| b-2 |
| 2 | ||
|
∴b2-2b-12=0,
∴b=1+
| 13 |
| 13 |
∴R(1+
| 13 |
| ||
| 2 |
即R的坐标为(1+
| 13 |
| ||
| 2 |
点评:此题主要考查反比例函数的性质,注意列方程组求出坐标点,列出方程是解题的关键,此题列出方程的依据有三角形的面积公式,有相似三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 针旋转90°得线段AB′.
针旋转90°得线段AB′. (2012•牡丹江)如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题:
(2012•牡丹江)如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题: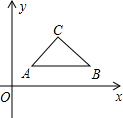 (2013•杭州一模)如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线
(2013•杭州一模)如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线