题目内容
 二次函数y=ax2+bx+c的图形如图所示,下列结论:①abc>0;②b2-4ac>0;③2a+b>0;④4a-2b+c<0.其中正确的是( )
二次函数y=ax2+bx+c的图形如图所示,下列结论:①abc>0;②b2-4ac>0;③2a+b>0;④4a-2b+c<0.其中正确的是( )| A、①② | B、②③ | C、③④ | D、①②③ |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b>0;由抛物线与x轴的交点个数,确定b2-4ac>0;当x=-2时,y=4a-2b+c.
解答:解:①∵开口向上,
∴a>0,
∵对称轴在y轴右侧,
∴-
>0,
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,故正确;
②抛物线与x轴有两个交点,
∴b2-4ac>0;故正确;
③∵对称轴x=-
<1,a>0,
∴-b<2a,
即2a+b>0;故正确;
④当x=-2时,y=4a-2b+c>0,故错误.
故选D.
∴a>0,
∵对称轴在y轴右侧,
∴-
| b |
| 2a |
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,故正确;
②抛物线与x轴有两个交点,
∴b2-4ac>0;故正确;
③∵对称轴x=-
| b |
| 2a |
∴-b<2a,
即2a+b>0;故正确;
④当x=-2时,y=4a-2b+c>0,故错误.
故选D.
点评:此题考查图象与二次函数系数之间的关系.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
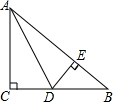 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,则斜边AB的长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△DEB的周长为10cm,则斜边AB的长为( )| A、8cm | B、10cm |
| C、12cm | D、20cm |
关于(
)11•211计算正确的是( )
| 1 |
| 2 |
| A、0 | B、1 | C、-1 | D、2 |
一个三角形的三边长分别是9cm,12cm,15cm,则这个三角形的面积是( )
| A、54cm2 |
| B、90cm2 |
| C、108cm2 |
| D、不能确定 |
有一个数值转换器原理如图,当输入的x的值为256时,输出的y的值为( )


| A、16 | ||
B、
| ||
C、
| ||
D、
|